3

I'm a bit confused about how to measure the oscillation period of a quasi-stable system when using the Ziegler-Nichols method to get the correct PID configuration. The factor of the oscillation period is used in the rule for the I and D terms, but in what unit? seconds, milliseconds, minutes? Does it have something to do with the sampling time of my digital PID controller?

Table of settings where Pcr is the "critical period"

Pcr is used here for describing the critical period (at the critical gain Kcr setting)

GregP
  • 5
  • 3
Evert
  • 309
  • 1
  • 3
  • 9
  • It's in seconds. This article explains it all very well: http://www.mstarlabs.com/control/znrule.html – akellyirl Jul 07 '14 at 14:40
  • My PID controller also has a variable sample time and that sampling time is in milliseconds, and it's used to calculate the factor of Ti (Ki = Kp * (Tsample/Ti)) So I guessed I need to refactor the period time (which can be measured in seconds) to the sampling time I used. For example: if I used a sampling time of 20 ms, and the oscillation period is 1 second, Ti should be: 1 * 1000 [ms] / 20 [/20ms], right? – Evert Jul 07 '14 at 14:56
  • My experience is that you'll drive yourself BATS trying to control a system with any complexity using a variable sample time. Do you really mean variable, or can you set it to be some constant in some range, but you can change that? – Scott Seidman Jul 07 '14 at 15:36
  • Yes, I mean the second part. so I can set the sample time to be 20 ms, or 1 second for example. After that it's fixed. But should there be a difference in the number I put in for Pcr in case of 20 ms sampling time, or, for example, 1 second sampling time. That's my main concern :) – Evert Jul 08 '14 at 06:48
  • I don't think sample time was considered when Z-N was developed (the original paper was published in 1942). – Spehro Pefhany Aug 07 '14 at 21:17

1 Answers1

2

The figure below shows the steps in order to find the \$K_{cr}\$(or \$K_u\$) and \$P_{cr}\$ (or \$P_u)\$, by changing the proportional gain only (with \$T_d=0\$ and \$T_i=\infty\$) - an example for temperature control:

PID ZN

The time unit to be used should be consistent with its response curve. The relationship with the sample period \$\Delta t\$ can be obtained, after the discretization of the PID controller. Using the standard form, in contrast with other implementations (for example, when the derivative term is taken from output):

$$u(t)=K_pe(t)+\frac{K_p}{T_i}\int_0^t{e(\tau)d\tau+K_pT_d\frac{de(t)}{dt}}$$

Taking the derivative of \$u(t)\$: $$u'(t)=K_pe'(t)+\frac{K_p}{T_i}e(t)+K_pT_de''(t)$$ A possible approach: To approximate the first and second derivatives using finite differences (eg backward), where \$k\$ is the sample id: $$x'(t)\approx\frac{x_k-x_{k-1}}{\Delta t}$$ $$x''(t)\approx\frac{x_k-2x_{k-1}+x_{k-2}}{\Delta t^2}$$ So, the discrete PID controller takes the form (velocity algorithm): $$u_k=u_{k-1}+K_p[(1+\frac{\Delta t}{T_i}+\frac{T_d}{\Delta t})e_k+(-1-\frac{2T_d}{\Delta t})e_{k-1}+\frac{T_d}{\Delta t}e_{k-2}]$$

Alternative definitions can include \$K_i=\frac{K_p}{T_i}\$ and \$K_d=K_pT_d\$. Also, the derivative term can be modified in order to reduce issues with high frequency noise - eg a low pass filter. Other discretization methods exist as well, such as Tustin, ZOH.

FURTHER EXPLANATION:

  1. Choose a sample time \$\Delta t\$ consistent with your process. There is extensive literature on the subject. For example, to avoid aliasing \$F_S > 2F_{BW}\$. In practice: Sampling frequency should be 10 to 30 times the bandwidth freq.

  2. Set \$K_p\$ to some low value (with \$T_i=\infty\$ and \$T_d=0\$ at this stage). So, the above equation is simplified to: $$u_k=u_{k-1}+K_p(e_k-e_{k-1})$$

  3. Implement the previous equation (a P controller) in your digital system along with that suitable \$\Delta t\$, testing \$K_p\$ to see if it causes continuum oscillation (marginally stable). If the oscillations decay, keep increasing \$K_p\$. If the oscillations increase in amplitude (unstable system), reduce \$K_p\$. Do this until the system is marginally stable. When you arrive at this point, you have found \$K_{cr}=K_p\$ and \$P_{cr}=\$oscillation period (see the figure above).

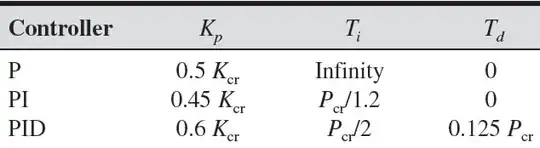
  4. Using the table you have provided (also above), determine the \$K_p\$, \$T_i\$ and \$T_d\$ values from the \$K_{cr}\$ and \$P_{cr}\$ ones.

  5. Implement the complete PID controller: $$u_k=u_{k-1}+K_p[(1+\frac{\Delta t}{T_i}+\frac{T_d}{\Delta t})e_k+(-1-\frac{2T_d}{\Delta t})e_{k-1}+\frac{T_d}{\Delta t}e_{k-2}]$$

Dirceu Rodrigues Jr
  • 3,210
  • 12
  • 17
  • I understand how the implementation of an PID controller works but for the Ziegler-Nichols method I need the oscillation period. So let's say my the oscillation period is 1 second and my sampling time is 1 sample/20ms, which value do I need to enter for Pcr? is that 1 or (1second/20ms) 50? – Evert Jul 09 '14 at 08:13
  • OK, then you know the step 5 described above. But please, pay attention to the step 3. In this case, considering that you applied that procedure and measured an oscillation period of 1 second, then Pcr = 1 second. The sample time appears explicitly on the complete equation for PID (not on P controller used for the ZN method - step 2). Of course, it assumes that you have chosen a suitable sample time value, for example << Pcr. – Dirceu Rodrigues Jr Jul 09 '14 at 14:32
  • Should this always work? I've run into some applications where setting incrementing Kp never produces a stable oscillation that leads to meaningful Ku/Tu parameters. Decrementing Kp gets a stable oscillation, but the ZN calculated PID params are nonsensical. – Cerin Oct 29 '16 at 01:13