Torque kgcm (what is kgcm)?

Question

I know what torque is but I find difficult to understand what Torque: 3kgcm means ?

I am not sure, how much weight that motor can carry, and I want to know how I can calculate that.

Please give me some hints :)

Yeap I got that, but is mining of that that that this motor can in theory carry max 3kg ? — Splendid, Mar 13 '12 at 00:05
More likely the maximum torque it can produce is (the force exerted on a 1 kg mass in a 1 g gravitational field) x (1 cm). Why they didn't use proper units is unclear, but many many people mix up mass with weight. — The Photon, Mar 13 '12 at 01:55
kg.cm should really be written as kgF.cm (kilograms-force . centimetres). kg is a measure of mass, kgF is a measure of force. — Li-aung Yip, Oct 23 '13 at 14:52
There are still ways to make it more confusing, for example, the "kilo" and the "centi" could be combined to "deka", giving us "dagm" as the new unit. — Simon Richter, Mar 04 '16 at 08:49
kg-cm is an abuse of metric, since kg is not a unit of force. changing it to 'kgF.cm' is an improvement, but the proper unit of force is the Newton ( = kg m /s^2), torque should be measured in Nm (newton-meter). 1 N-m = 0.7376 foot-lbf. — greggo, Dec 28 '16 at 20:53
The torque 3 kg-cm depends what planet you are on. On the surface of Jupiter, for example, it is a lot of torque. On the surface of Phobos, it is not very much. And if you are in space with your propulsion and warp drive turned off, it is no torque at all. — richard1941, Oct 22 '18 at 18:29

Russell McMahon · Accepted Answer · 2020-06-27T07:12:16.963

31

Torque is a measure of "twisting force".
Power is a measure of twisting force x speed.

Torque is usually expressed as a Force x a distance So for the same Torque if you double the distance you halve the force to get the same answer.

So kg.cm is kg force x centimetre distance.
In fact kg is a unit of mass and not of force BUT kg is sloppily used as unit of force in many cases.

Other torque units include foot-pound, Newton-metre, dyne-centimeter (!) ...

In your case 3 kg.cm means that a "force" of 3 kg acting at a radius of 1 cm would produce the same amount of torque as your motor.
Equally that could be 0.1 kg x 30 cm, or 10 kg x 0.3 cm or ...

FWIW - kg is a unit of mass and Newton the corresponding unit of force. Where the "weight" of 1 kg = g Newton where g = 9.8 m/s/s. Close enough g = 10 here so 1 kg weighs 10 Newton.

BUT pound IS in fact a unit of force.
The corresponding unit of mass is the Slug where
1 Slug weighs ~32 pounds force.
You will not find people selling vegetables by the slug, or by the Newton :-).
A Newton glass of beer is about 4 ounces.

A useful approximation

Power in Watts ~= kg.m torgue x RPM

This is just happenstance as various constants cancel almost exactly but it is extremely useful. Accurate to about 1%.

So in your case 3 kg.cm = 0.03 kg.m
So the power that your motor makes at a given RPM at this torque is
Power = 0.03 x RPM Watts.
ie about 30 Watts at 1000 RPM at 3 kg.cm torque.

I have spent many long hours playing with dynamometers while developing alternator brakes and controllers to act as loads for exercise equipment.
The approximation

Watts = kg.m.RPM ......was a useful approximation to remember.

edited Jun 27 '20 at 07:12

answered Mar 13 '12 at 01:53

Russell McMahon

150,303
18
213
391

3

It may be helpful to note that while the units for torque and work may appear similar, the force and distance vectors related to torque are always perpendicular, while those for work are always parallel. Torque is the cross product of the force and a distance vector between the applied force and the pivot point, and is thus a vector; work is the dot product of the force on an object and a distance vector representing its motion; it is thus a directionless quantity. – supercat May 30 '13 at 17:40
Actually it's not a good idea to measure goods by weight as weight per mass is not a constant (not only compared on different celestial bodies but also on different locations on earth): 10N of vegetables near the equator have more mass than 10N of vegetables near the poles. – Curd Jan 13 '17 at 15:30
@Curd Usually :-). Note the "not for trade" labels on many spring based weighing systems and the use of ratiometric weight against unit weight weighing systems to cancel out g variations. The situation is worse on the Moon due to Masscons - but there are liable to be greater concerns there. I think the distinction is made as well in the above as it's liable to be in the circumstances. For extra points argue for or against expressing rocket motor fuel efficiency term "Specific Impulse" in 'seconds'. To do this you need to cancel lbf with lbm (or kgf with kgm or other unit of your choice) :-). – Russell McMahon Jan 13 '17 at 17:17
watt = kg.m.RPM/10 is a useful approximation since P = Tw (not T rpm) and w <=> RPM is a factor if pi/30 = 0.104719 ~ 0.1 for quick calcs – Jun 27 '20 at 09:09
1

@JonRB My original formula is correct. You have perhaps missed g (9.8 m/s/s) on the top line which ~~= cancels with your 10. || Power ~= Kg.m torque x RPM. || Real power = F x d /time = kg x g x 2 Pi x R x RPM/60 = (kg.R. RPM) x (2.g.Pi/60) and 2.g.Pi ~~= 60. Yes? || The Power ~= kg.m.RPM works very nicely and I have used it extensively. – Russell McMahon Jun 27 '20 at 11:55

score 31 · Answer 2 · edited Sep 02 '17 at 12:01

31

A motor with 1 kg.cm torque is capable of holding a 1 kg weight at a radial distance of 1 cm.

Here is a diagram to explain.

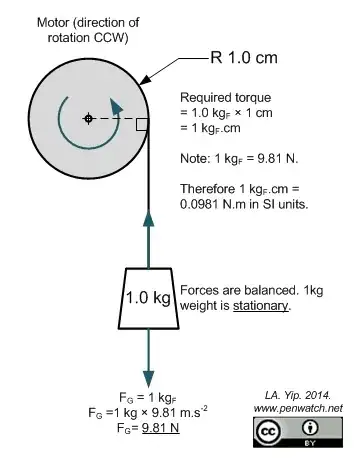
enter image description here

Torque is the cross-product of force and distance: \$ \tau = F \times d \$. So the same weight, at twice the radial distance, will require double the torque.

enter image description here

Note that the measurement 'kgcm' is 'kilograms-force × centimetres' and would be clearer if written as \$ kg_F.cm \$, which avoids confusion between kg (mass) and \$ kg_F \$ (force.)

The \$ kg_F \$ unit is not used for engineering work any more because \$ 1 kg_F \$ is defined as the force on a 1 kg weight in 'standard Earth sea-level gravity', but no-one can agree on a precise value for 'standard Earth sea-level gravity'. Plus, it's not a very intuitive unit when you aren't on Earth.

The SI unit of N.m, which doesn't depend on the exact value of Earth gravity, is preferred instead.

edited Sep 02 '17 at 12:01

Prasan Dutt

286
2
15

answered Feb 06 '14 at 02:44

Li-aung Yip

9,001
28
51

2

What planet are we talking about-- Jupiter, or Luna? – richard1941 Oct 15 '17 at 01:14
@richard1941 Your concerns are addressed further on in the answer. "The kgF unit is not used for engineering work any more because 1kgF is defined as the force on a 1 kg weight in 'standard Earth sea-level gravity'..." – Li-aung Yip Oct 17 '17 at 00:39
The diagrams make it so much easier to understand. – Hentie Potgieter Oct 30 '19 at 11:16
@Li-aung Yip, how is the weight stationary in the second case? Wouldn't the torque be higher than the force due to the 1kg mass? So the weight would actually move up, right? – penguin99 Dec 11 '19 at 06:15

score 8 · Answer 3 · answered Mar 13 '12 at 00:23

8

kgcm would be kilogram-centimeters, the motor is very old or the manufacturer does not like SI units. Anyway, 1kgcm is 0.09807Nm.

The weight that your motor will be able to lift will depend on how big the pulley is. If the pulley is 2cm diameter (1cm radius) the motor will be able to lift 3kg. If the pulley is 20cm, the motor will be able to lift ~300g.

If you want to lift more than that, you need a gearbox that reduces the speed, but increases the torque.

answered Mar 13 '12 at 00:23

Pentium100

6,610
3
35
40

Thanks, I understand better now, now I need to calculate stuff for my wheels :) – Splendid Mar 13 '12 at 01:57
1

Huh. I thought kgcm was the way the world was going now. I keep seeing it pop up everywhere these days. I used to see more Nm, but that seems to be fading away. – Brian Knoblauch May 30 '13 at 12:36
1

@BrianKnoblauch - well, with SI insisting that 1024 bytes must be called a kibbidibibidibibibyte, I feel I must insist on newton-meters. =) – JustJeff May 31 '13 at 01:36
Nothing against NM, I prefer it. It just seems to be fading away from what I've seen. – Brian Knoblauch May 31 '13 at 12:26
I'm also seeing 'kg-cm' - in a servo spec most recently - but it's still just plain wrong. Confusion between mass and force in the imperial measurements is not mitigated at all by making the same error in metric, where there are distinct units for these. Decades ago, I owned a torque wrench, the scale was calibrated in "foot pounds" and "metric kilograms". Never even tried to figure out what that was supposed to be. I've also seen oil pressure gauges in "kg/cm^2". Arggg. That's a measure of fertilizer application rate, not pressure. – greggo Dec 28 '16 at 20:29
Also, there may be a limitation on the amount of force the motor bearing can support. It may have nothing to do with the torque generated by magnetic fields inside the motor. – richard1941 Oct 15 '17 at 01:15

score 2 · Answer 4 · answered Mar 13 '12 at 01:01

Torque is a measure of force times distance. Think of turning a nut with a wrench: the further out the wrench you pull, the easier it is to turn the nut. This is because the same force, further out the handle, gives higher torque, because it has to apply that same force over a longer movement distance to do the work. A gearbox also uses the same principle, it's a way to exchange distance from center for distance of movement to step up the torque.

US units are dumb, because they use the same unit ("pound") for both force and mass, even though they are different. SI units are better, because they use one unit (kilograms) for mass, and another unit (Newtons) for force. A kilogram of mass will typically exert 9.81 Newtons towards the center of the Earth under normalized gravity (varying depending on where you are.)

I've seen a lot of motors with torque expressed in kgcm, and I don't quite understand why that is. Perhaps someone translated pound-inches (or the 12 times stronger foot-pounds) and used the wrong destination unit at some point, and the convention stuck. In countries that use real SI units, you want torque in Newton-meters, and if you have small stepper motors or whatnot, you may get Newton-centimeters.

So, can your motor hold 3 kg? Yes, if the distance between the center of the axle, and the center of mass it's holding, projected along the axis of gravity to the plane of the axle, is 1 cm or less. If the distance between center of driveshaft and center of mass is longer, then you need a gearbox, or a lighter load, or a stronger motor.

torque actually the cross product, work is the scalar product — russ_hensel, Mar 13 '12 at 12:56
In engineering work, when dealing with pounds, it's common to use lbf and lbm to distinguish force and mass, so torque is actually in ft-lbf. Failing to make this distinction results in abominations like torque in 'kg-cm' and pressure in 'kg/cm^2'. So when faced with a torque spec given in oz-in and kg-cm, you have a choice between the one with a vague unit (oz) and the one with incorrect dimensions (kg instead of N). Not a good situation, I wish people would use metric correctly. — greggo, Dec 28 '16 at 20:37
US units are dumb because we got them from ... . Actually, everything in science and electrical engineering here is metric, and our money is decimal — richard1941, Jul 24 '17 at 10:41
FWIW - the "US" unit of mass is the Slug, which has a mass of which weighs g lbs or about 32 lbs in a "standard" gravity field. — Russell McMahon, Apr 08 '18 at 23:59

score 1 · Answer 5 · answered Sep 11 '18 at 20:00

The best way I use to test stepper motors is just using a known diameter pulley, hold the motor in the corner of the table with a vise, wrap a wire in the pulley and tie a container (plastic small bucket) at the end of the wire, run the motor to move the bucket up and down while slowly applying weight into the bucket until the motor could not lift it anymore. Normally I use screws, bolts, nuts, heavy metal parts as weight. When the motor stalls, I remove some until the motor is able to lift the bucket again. The total weight (kg) of the bucket multiplied by the radius (cm) of the pulley, badabim, there is the torque of the motor in kgf-cm. Also, by doing that you can test different ways to drive the motor, with PWM or microstepping, and see different torque responses from the motor.

score -1 · Answer 6 · answered Jan 24 '16 at 06:20

There is nothing "sloppy" about using kg/pound/ounce/gram for both mass and force simultaneously as long as you recall that torque is rotational.

A kilogram-meter torque can move (twist) a kilogram held at a fixed radius of 1 meter (or half that at 2 meters). A pound-foot torque can move (twist) a pound held at fixed radius of 1 foot (or half that at 2 feet). An ounce-inch torque can move (twist) an ounce held at a fixed radius of 1 inch (or half that at 2 inches).

All of the units of torque: kg.cm, lb.ft, oz.in, g.cm can all very easily be thought of as the amount of torque needed to move a point mass of the stated weight on the edge of a disc being spun by the motor that has the torque rating. Rather than the example of suspending the mass above, think of the mass on the edge of the disc going around as the motor drives the disc around. Not all motors can move all masses on these discs. Only the motor whose torque is equal to the mass times the radius of the disc can be moved. If a 3 kg mass is at one point on the perimeter of a disc of radius r cm, then in order for that disc to be turned, the motor must have a torque of 3r kg.cm.

Is the last sentence correct? For a horizontal (ideal, frictionless) disc any load could be turned with any torque. The acceleration would be proportional to the torque, would it not? — Transistor, Jan 24 '16 at 09:05
Yes, it's sloppy. kg is not a unit of force. lbf is a unit of force (which converts to N). lbm is a unit of mass (which converts to kg). Confusing those two is sloppy too (but happens all the time). As @Transistor has pointed out, your entire discussion assumes that standard gravity is acting in a tangential direction, which is only true if the axis of the wheel is horizontal and the 3 kg mass is at the point where it is moving up. The advantage of stating the torque (properly) in terms of force, is that you can easily apply the calculation to other situations (force due to a spring, e.g.) — greggo, Dec 28 '16 at 20:57

score -1 · Answer 7 · answered Mar 04 '16 at 07:40

If you are having problems because of the metric unit, then changing them to English units might help. As a "first approximation," a kg = 2 lb, and 2.5 cm = 1 in. So 3kgcm would be (3 x 2) / 2.5 = 2.4 lb-in. If you use a 2in diameter pulley, you would be able to exert/hold a 2.4 lb force.

Torque kgcm (what is kgcm)?

7 Answers7

Linked