3

In the figure, if I = 80 mA, determine the resistance R.

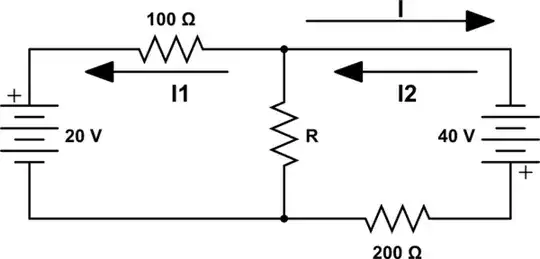
schematic

simulate this circuit – Schematic created using CircuitLab

Answer is 600Ohm.

My Steps :

$$ I2=-0.08$$ $$20+R\left(I1-I2\right)+100I1=0\tag1$$ $$200I2+40+R\left(I2-I1\right)=0\tag2$$

So $$20+R\left(I1+0.08\right)+100I1=0\tag1$$ $$24-R\left(I1+0.08\right)=0\tag2$$

Then $$ R\left(I1+0.08\right)=24\tag{a} $$

Now I sub (a) to (1) and get $$ 20+24+100I1=0\\ 100I1=-44$$ $$I1=-0.44\tag{b} $$

Sub (b) back to (a), $$ R\left(-0.44+0.08\right)=24\\ R=-66.67 \Omega\\ $$

How to obtain the answer 600 Ohm?

Ricardo
  • 6,164
  • 20
  • 53
  • 89
Casper
  • 297
  • 2
  • 6
  • 19

2 Answers2

5

The answer is definitely wrong. Here's a quick way to tell. If you have R=infinite, then you have 40V/300ohms = 0.133 amps if you ignore current provided by the 20V supply. That's the absolute minimum current that will flow through I. Any lowering of R from infinite will only increase the amount of current flowing through I. That means that their initial statement of I=80mA is impossible.

The only exception to that is if we do allow negative resistances as you have calculated. A negative resistance would be kind of like a voltage/current source. You're likely correct in your negative resistance calculation.

horta
  • 12,818
  • 23
  • 45
  • If R is infinite, there's 60V / 300 ohms. – Ben Voigt Jun 26 '14 at 21:25
  • @BenVoigt I originally used 60V, but that voltage could potentially drop as R lowers from infinite due to the 20V dropping across it, so it's more solid to ignore the other 20V because it only adds to the current. 40V/300 still is way above the 80mA the problem offers. – horta Jun 26 '14 at 21:33
  • To be sure, the current $I$ is independent of $R$ and equal to $200\mathrm{mA}$ except for the special case $R = -\frac{200}{3}\Omega$ which allows $I$ to be any value. – Alfred Centauri Jun 26 '14 at 22:29
  • @AlfredCentauri Understood, your way is definitely the proper way to do it. My way is simply a sanity check. – horta Jun 27 '14 at 00:03
  • 1
    @horta, I'm all for sanity checks and I do understand your calculation and superposition like approach. The 20V source can only increase the current so you've set a lower bound on $I$ (assuming $R \ge 0$). – Alfred Centauri Jun 27 '14 at 00:19
3

Actually, in this circuit, the current \$I\$ is independent of the resistance \$R\$.

To see this, remove \$R\$ from the circuit and calculate \$I\$:

$$I = \frac{20V + 40V}{100\Omega + 200 \Omega} = 200\mathrm{mA}$$

Interestingly, this implies that the voltage between the nodes where \$R\$ was connected is:

$$20V - 200\mathrm{mA} \cdot 100 \Omega = 0V$$

This means that we can add \$R\$ back to the circuit and the solution doesn't change since there is no voltage between those nodes.

Thus, there is no value of \$R \ge 0\$ that will yield a current \$I = 80\mathrm{mA}\$.

However, if we allow \$R < 0\$, we have the interesting possibility of an infinity of solutions!

Writing a KCL equation at the top of \$R\$ yields

$$\frac{V_R}{R||100\Omega||200\Omega} = 0A$$

For \$R\ge 0\$, the only solution is \$V_R = 0\$ as derived above.

But, if we allow

$$R = - (100\Omega||200\Omega) = -66.67 \Omega$$

the denominator is infinite and thus, there is a solution for any \$V_R\$ and associated \$I\$!

This shouldn't actually be too surprising. The Thevenin equivalent circuit 'seen' by the resistor \$R\$ is given by

\$V_t = 0V\$

and

\$R_t = 100||200 \Omega = 66.67 \Omega\$

If we then parallel this equivalent circuit with an \$R = -66.67 \Omega\$ resistor, the new Thevenin equivalent becomes an open circuit.

This means that we can place a voltage source across \$R\$ and the voltage source will not supply any current.

In other words, we can temporarily place a voltage source across \$R\$ and, since the source supplies no current, remove the source and the voltage across \$R\$ will not change - the circuit will maintain that voltage across \$R\$.

Of course, there are no physical negative resistors (though we can approximate them with active circuits) so this is mostly academic.

Alfred Centauri
  • 26,630
  • 1
  • 25
  • 63