How would I solve this Block Model diagram of a DC motor?

Question

Sorry if this website isn't the place for this question but I am really lost on how to solve this and I'm being tested over it tomorrow.

I somehow keep on getting the answer 475 instead of the correct one, 425. How would I go about solving this? I think the main place I'm getting lost is dealing with the 1/s block. What do I do with that? One of my friends said that I should just consider s as converging to 0 and treat it as if it was indeed zero.

Answer 1

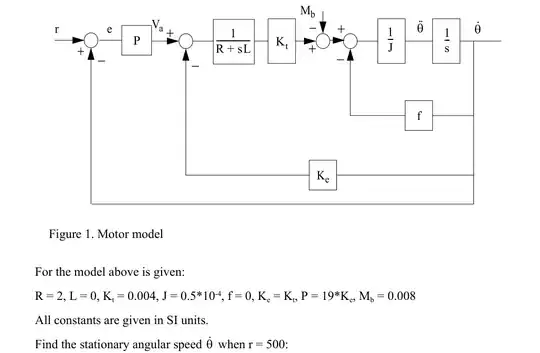
You cannot treat the 1/s blocks as just converging to zero. These are integrator blocks as this model is being represented in the s-domain, the integral domain (laplace). You can however treat the "s" that is part of sL as tending to zero as it represent an inductor. Equally L = 0 so that \$\frac{1}{r + sL}\$ becomes 1/R

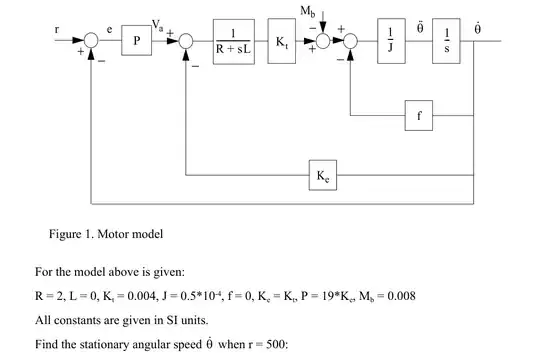
So it is a simple representation of a speed controller.

• You have a speed demand coming in and an error block to provide a speed error.
• This speed error is applied to a proportional gain of 19* the backEMF constant. The output of which is a voltage demand. This is the end of the speed controller, the rest is the motor model.
• You have an error block that takes the voltage demand & subtracts the "voltage feedback", the terminal voltage of the machine This provides the forcing voltage.
• A 1/(R+sL) is a 2nd order representation of a machines stator (R+L) and the output is the current that would flow.
• With a stator current generated it is passed through a gain block, with a gain of Kt and the output is then EM-TORQUE.
• Another error block with an input of Mb, at a guess I would say mechanical bearing torque.
• The output is then shaft torque.
• Another error block to provide the ability to load the machine (speed dependent load, maybe a fan?)
• a 1/J block will take a TORQUE and produce ACCELERATION.
• a 1/s block will take this ACCELERATION and integrate it to produce speed.
• This shaft speed is then fed back into the control loops to provide
  1. speed-dependent backEMF
  2. speed feedback.

So to analyse this in a steady-state situation:

ASSUME the system has stabilized at no-load speed (as f=0) so the speed feedback = the speed demand = 500. However... from the additional infomation provided, the controller cannot reach such a speed demand, the added bearing torque has loaded it enough.

For no more acceleration the output of the Mb error block must be zero and thus the output of Kt = Mb = 0.008Nm So the current must be = 2A

With a stator inductance of 0 & with the sL part generally tending to zero (for steady state) the voltage applied to the terminals needs to be 4V

It has now been reduced to a simple 1st order equation concentrated around the 1st two error blocks. This can be written as

\$(r-\omega)*P = V_a \$

\$ V_{error} = V_a - \omega*K_e \$ Where \$V_{error} = 4\$ from previous calcs.

\$(r - \omega)*P = 4+\omega*k_e\$

\$P*r -4 = \omega*k_e + P*\omega\$

\$(P*r-4)/(k_e+P) = \omega\$

ergo: \$\omega = 425\$

Answer 2

How did you arrive at your answer (475)?

My approach for solving the problem would be (first step) to find the overall transfer function in the s-domain. This shouldn`t be a big problem because we only have two feedback loops (for f=0): One inner and one overall (outer) loop. As a second step, you could apply the final value theorem which gives you the output in the time domain (after transients have been settled).