Complex multiplication identity

Question

From my EM theory book:

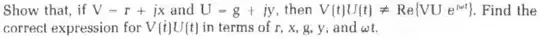
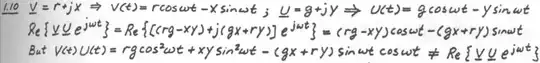
I have the solution for this problem, but I don't even understand the first step. How does \$V = r + jx \implies v(t) = rcos(wt) - xsin(wt) \$??

Answer 1

The formula to convert from the phasor representation \$V=r+jx\$ to its time-domain equivalent is this:

\$ V(t) = Re\{V \, e^{\,j\omega t}\} \$

Using the complex identity:

\$ e^{\,j\omega t} = \cos(\omega t) + j\,\sin(\omega t) \$

You obtain:

\begin{align*} V(t) &= Re\{V \, e^{\,j\omega t}\} = Re\{ (r+jx) \cdot [\cos(\omega t) + j\,\sin(\omega t)] \} = \\[1em] &= Re\{ r \cos(\omega t) - x \sin(\omega t) + j[...] \} = \\[1 em] &= r \cos(\omega t) - x \sin(\omega t) \end{align*}