Find charge per unit length of conductors

Question

Sorry if off-topic but I have a question in electrostatics. I didn't get any usefull answer at physics forums. The problem states:

Three very long (theoretically infinite long) hollow cylindrical conductors, with radius a,b,c,(c>b>a) are in vacuum. Inner and central conductor are charged, and outer conductor is grounded. Potentials of inner and central conductors with reference point relative to outer conductor are Va,Vb. Find charge per unit length of all three conductors.

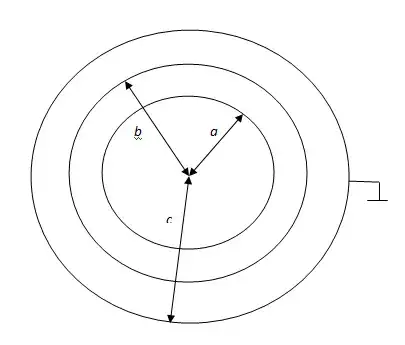
I used Gauss's law to find electric field of one cylindrical conductor, which is $$E=\frac{\lambda}{2\pi r \epsilon_0}$$ Derivation of Va gives $$V_a=\int_a^b \frac{\lambda_a}{2\pi r \epsilon_0}dr+\int_b^c \frac{\lambda_a}{2\pi r \epsilon_0}dr=\frac{\lambda_a}{2\pi \epsilon_0}\left(ln\frac{b}{a}+ln\frac{c}{b}\right)$$ Derivation of Vb gives $$V_b=\int_b^c \frac{\lambda_b}{2\pi \epsilon_0 r}dr=\frac{\lambda_b}{2\pi\epsilon_0}ln\frac{c}{b}$$ Now, charges per unit length for first two conductors are $$\lambda_a=\frac{2\pi\epsilon_0 V_a}{ln\frac{b}{a}+ln\frac{c}{b}}$$ $$\lambda_b=\frac{2\pi\epsilon_0 V_b}{ln\frac{c}{b}}$$ Using superposition, charge per unit length of third conductor is $$\lambda_c=\lambda_a+\lambda_b$$ Could someone check if this is correct? I am not sure if the limits of integration for potentials are right.

Thanks for replies.

Answer 1

This is a nice question...

Let's start with your last statement. It must be

$$\lambda_c=-(\lambda_a+\lambda_b)$$

because cylinder C has to cancel out the charges of cylinders A and B.

Now, think about the fields generated by the three charges. It looks like this:

Remember, that the charge on a conducting, hollow body does not generate any E-field inside.
But the E-field of a charge inside a hollow body does not end at the surface, it expands to infinity.
This also is a result of Gauß' law, as it simply says that field times (closed) surface is charge inside that surface.

The superposition of all fields is the grey curve, and now you see that

$$V_b=\int_b^c\frac{(\lambda_a+\lambda_b)}{2\pi\varepsilon_0r}\,dr$$

and

$$V_a=\int_a^b\frac{\lambda_a}{2\pi\varepsilon_0r}\,dr+V_b$$

With given potential(difference)s, you can calculate \$\lambda_a\$ and \$\lambda_b\$.