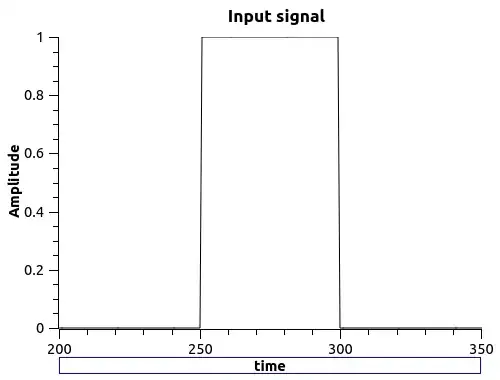
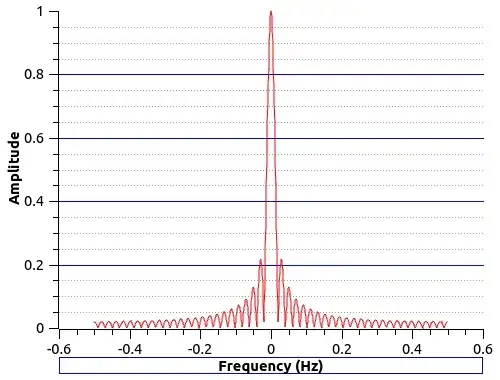
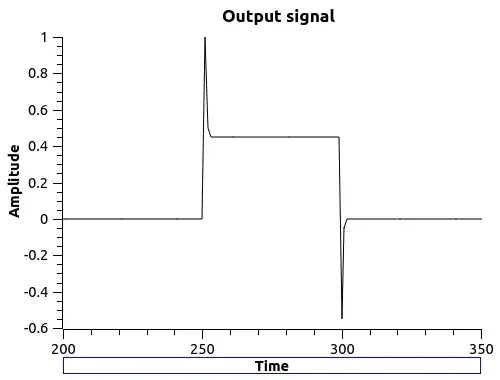
The bode plot itself is built based on a transfer function, regardless of the input signal that will excite the circuit. Based on what I've learned, the bode plot show us how the response amplitude and phase will react when we change the input's frequency.
However, I can only understand the meaning of the plot when the input is a sinusoidal signal. When the input is a non-periodic function, I can't see what would be the meaning of the bode plot, since I can't understand how would be possible to change the "frequency" of a non-periodic function.
So, my question is: Is the bode plot only meaningful when we are analysing a circuit that is excited by a periodic signal? If not, what would be the meaning of the "frequency" (x-axis) of the plot when the input is non-periodic?
I'm a bit confused because I always see bode plot examples when the instructor draw the bode plot of any transfer function, without caring if the circuit will be excited by a period function or not.
Thank you !