3

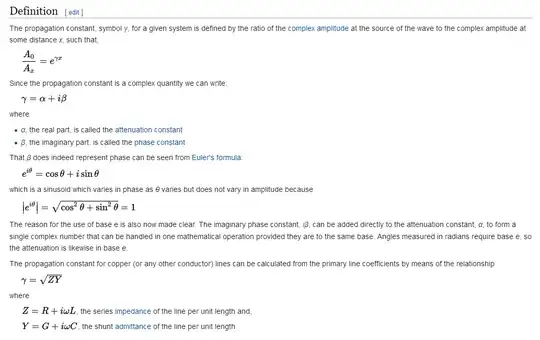
In Does conductance in the transmission line model represent a physical quantity? it came up that a non-real characteristic impedance just means the line has some loss. With real transmission lines having a little (but perhaps negligible) loss, we could expect all real transmission lines to have a characteristic impedance with at least a small imaginary component.

But is that really true? Let's say \$Z = Y = 1+1j\$. The characteristic impedance of this line is real:

$$ \sqrt{ 1+1j \over 1+1j } = 1 $$

And the attenuation constant is 1 [corrected by edit]:

$$ \operatorname{Re}\sqrt{(1+1j)(1+1j)} = 1 $$

Which to my understanding, means this line is lossless. But how can this be when it has both a non-zero conductance and resistance?

Community
  • 1
Phil Frost
  • 57,310
  • 18
  • 145
  • 267

1 Answers1

1

Phil, the real part of the propagation constant is the attenuation constant and this equals: -

\$Re\sqrt{(R+jwL)(G+jwC)}\$ and not the formula you have in your question.

The formula you have used is for characteristic impedance.

This wiki page should confirm this (right at the bottom): -

enter image description here

So, if you do the math at low frequencies (to make life easier) you see that the attenuation constant becomes \$\sqrt{RG}\$ and if R=G=1 then you have a constant of 1 and a lousy highly lossy line. A lossless line has a re(propagation constant) of zero.

Andy aka
  • 456,226
  • 28
  • 367
  • 807
  • 1
    Both the series R and parallel G are resistive and therefore loss components. – skvery Mar 16 '17 at 16:59
  • 1
    Both the questioner and I know that but, the question is all about the real part of the propagation coefficient. – Andy aka Mar 16 '17 at 17:19
  • Ah whoops, that was a typo. But isn't $\sqrt{(1+1j)(1+1j)} = 1+1j$ still? – Phil Frost Mar 16 '17 at 18:41
  • At DC the attenuation constant is $\sqrt{RG}$ and if R=G=1 then the constant is 1 and therefore this is a big loss. It isn't lossless - it may be that you are confusing distortionless for lossless? A lossless line will have a constant of zero. See this: https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=1&ved=0ahUKEwjqnPHo9dvSAhWLCsAKHXO4ChkQFggcMAA&url=http%3A%2F%2Fwww.ittc.ku.edu%2F~jstiles%2F723%2Fhandouts%2FThe_Lossless_Transmission_Line.pdf&usg=AFQjCNGGX8VR_Sv63vv0c9eRh37u-iYfqQ&sig2=aRArjDbeR3RnbXCDLU7Rag&cad=rja – Andy aka Mar 16 '17 at 21:02