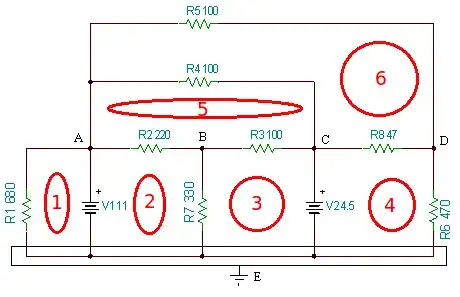
Hi I'm having a really bad time in analyzing this 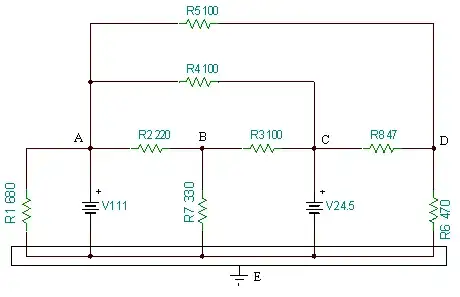
I can't seem to establish the node equations, I've been reading on articles on how to solve it but the majority use current sources and the methods differ quite a bit, any help is really appreciated.
I know that I have to use KCL on each node, for example for node B I said:
\$ I_{1}+ I_{2} - I_{3} = 0 \$
\$ I_{1} = \dfrac{A-B}{220} \$
\$ I_{2} = \dfrac{C-B}{100} \$
\$ I_{3} = \dfrac{B}{330} \$
Given that and solving for B
A = 12 v
C = 4.5 v
\$ \dfrac{A-B}{220} + \dfrac{C-B}{100} - \dfrac{B}{330} = 0 \$
\$ \dfrac{A}{220} - \dfrac{B}{220} + \dfrac{C}{100} - \dfrac{B}{100} - \dfrac{B}{330} = 0 \$
\$ \dfrac{A}{220} + \dfrac{C}{100} - B ( \dfrac{1}{220} + \dfrac{1}{100} + \dfrac{1}{330}) = 0 \$
\$ \dfrac{A}{220} + \dfrac{C}{100} = \dfrac{B}{\dfrac{1}{220} + \dfrac{1}{100} + \dfrac{1}{330}} \$
B = 650( A/220 + C/100 )
Substituting A=12, C=4.5
\$ B = \dfrac{ \dfrac{A}{220} + \dfrac{C}{100 } }{ \left( \dfrac{1}{200} + \dfrac{1}{330} + \dfrac{1}{100} \right) } \$
B = 5.66 v
because of independent voltage sources.
I know my problem is on establishing the equations as I don't fully grasp how the analysis is made.