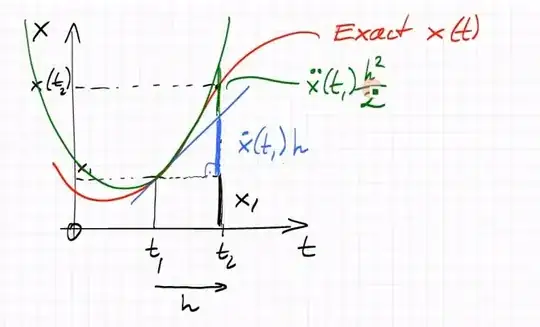
Suppose we're given the position \$x\$ , velocity \$\dot{x}\$ , and acceleration \$\ddot{x}\$ at \$t_1 \$.
We need to approximate the position \$x\$ at \$t_2\$.
In below picture, I understand how \$x_1\$ represents the vertical black length, and how \$ \color{blue}{\dot{x_1}(t_1)}h\$ represents the vertical blue length. However I don't get how \$\color{green}{\ddot{x}(t_1)}\dfrac{h^2}{2}\$ represents the green length. I'm wondering if there a simple derivation for proving that the green vertical length equals \$\color{green}{\ddot{x}(t_1)}\dfrac{h^2}{2}\$ . Any ideas ? Thanks !