4

I have an oscillator producing a sine wave with amplitude 3 V (so it oscillates between +3 V and -3 V). The oscillator is at about 500 Hz. I connected this to an 8 ohm speaker and I hear the sound from the oscillator. I noticed that on the speaker is written 0.5W, so I assume that this speaker can handle at most 0.5 W.

I am not sure that I understand how speakers work, but applying Ohms law I see that at 3 V and 8 Ohm, the speaker would draw a current of 3/ 8 = 375 mA. This would mean that the power consumed is P = UI = 3x 0.375 = 1.125 W.

The speaker is only rated for 0.5 W, so I assume that I should reduce the amplitude if I don't want to damage the speaker.

My question is simply: Did I calculate this correctly?

(One of my concerns is if I can apply Ohms law since the voltage isn't constant. Could I possibly just add a resistor in series with the speaker to increase the impedance?)

Thomas
  • 229
  • 3
  • 9

2 Answers2

2

First, your Ohm's Law equation is calculating what is called 'peak power,' which uses the maximum voltage output of the amplifier. Another common way to specify power ratings on speakers is 'RMS power,' which calculates the equivalent heating of a DC source as your AC source (i.e. the amplifier). RMS power of your setup would be:

$$P_{RMS} = V_{RMS}^2 / Z_{speaker} = \frac{V_{peak}^2}{2} / Z_{speaker}$$

So in your case, the \$3 V_{peak}\$ amplitude reduces to \$2.12 V_{RMS}\$ You'll need the datasheet of your speaker to determine whether the 0.5 W rating is in peak or RMS power.

But that's not the whole story, because \$Z_{speaker}\$ is certainly more than just a DC resistance. Alluding to this previous question, the speaker is modeled as a combination of DC resistance with a significant inductance in series, plus some parasitic components:

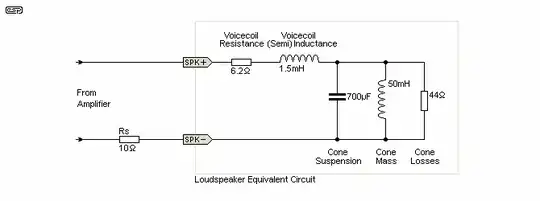
Speaker model

(Note that Andy's answer's link has moved here as of this posting.) Recall that the impedance of an inductor increases as frequency increases:

$$Z_{inductor} = j \omega L = j 2 \pi f L $$

So the speaker's impedance will also vary with frequency. From my experience, speaker impedance is often rated at 1 kHz or thereabouts, so your speaker's impedance at 500 Hz may be lower and thus more power may be delivered than you'd calculate by using the static \$8 \Omega\$ value.

There is also the question of your amplifier's output impedance. If you see \$3 V_{peak}\$ with the amplifier unloaded, even \$1 \Omega\$ of output impedance (a very fine amplifier indeed) will reduce the voltage across the speaker to \$1.88 V_{RMS}\$ and thus reduce the power delivered to the speaker.

My suggestion: observe the voltage across the speaker and listen for any distortion, which is a good indication of over-driving. And examine the datasheet if you have it.

calcium3000
  • 2,516
  • 1
  • 16
  • 43
  • Ok, so if I observe the voltage over the speaker with an oscilloscope when everything is connected I should get an idea of the "true" peak-to-peak voltage? – Thomas Aug 10 '18 at 16:30
  • @Thomas Yes. If you want to be safe, connect a small-valued resistor (about $1 \Omega$) in series with the speaker first to observe how the amplifier voltage reacts. If it drops half a Volt or so you should be in the clear. – calcium3000 Aug 10 '18 at 16:37
  • Quick follow up question: How did you calculate the $1.88V_{RMS}$ from $3V_{RMS}$ with the load of $1$ Ohm? – Thomas Aug 12 '18 at 00:32
  • 1
    @Thomas Apologies -- I used a simple voltage divider calculation: $V_{out} \frac{Z_{speaker}}{Z_{speaker} + R_{out}} = 2.12 V_{RMS} \frac{8 \Omega}{8 \Omega + 1 \Omega} = 1.88 V_{RMS}$ – calcium3000 Aug 12 '18 at 01:50
  • No need to apologize. Thank you for the answer and clarification :) – Thomas Aug 12 '18 at 01:52
1

If your signal is 3 volts peak, it will only be 2.1 volts RMS.

2.1 volts RMS into 8 Ohms is about 0.55 watts, so, at first glance, you are only slightly overdriving the speaker.

However, the source resistance of the circuit providing the signal must also be considered - is the actual voltage across the speaker really 2.1 volts RMS (6 volts peak-to-peak)?

Peter Bennett
  • 59,212
  • 1
  • 49
  • 132
  • I am not sure what the source resistance is. The source is an synthesizer and I am using the headphone output. If I measure the output on my oscilloscope, I have 6 V peak-to-peak. I haven't measured it when connecting the speaker. – Thomas Aug 10 '18 at 16:15