Why is the voltage \$ V_A = 2.5V \$ in this circuit?
I know the current in the mesh by applying KVL is:
\$ I = 50 \mu A \$
but why is
\$ V_A = \dfrac{V_1}{2} + \dfrac{V_2}{2}\$?
How do the voltages V1 and V2 end up being added together? Could you explain this to me with equations?
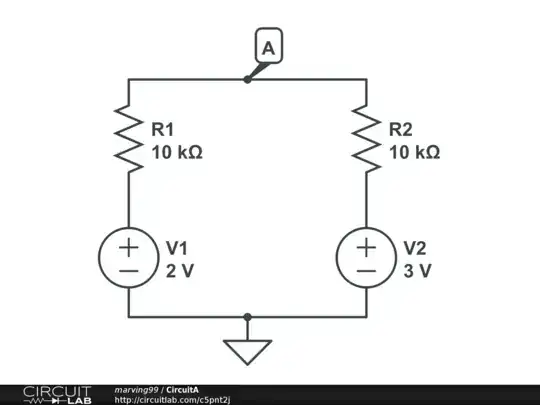
You choose a direction to walk through the maze, let's say clockwise. Starting from ground we first encounter a 2 V voltage source, so after that we're at +2 V. You already calculated the current of 50 µA, and that's flowing counterclockwise because we have the higher voltage at the right side.
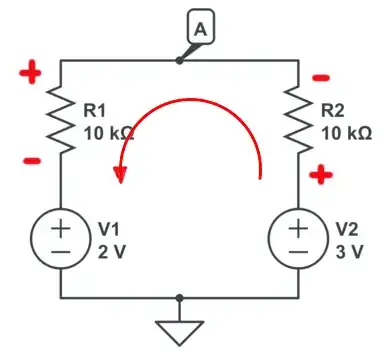
So the resistor will have a 50 µA \$\times\$ 10 kΩ = 500 mV drop across it (Ohm's Law), and we're going against the current, so we're going from the lower voltage to the higher, which means we have to add the 500 mV to the 2 V we had already. So we arrive at A with 2 V + 500 mV = 2.5 V. If you would have started with the 3 V and went counterclockwise you would have had 3 V = 500 mV = 2.5 V.
Note that if you have 2 different voltages connected by two equal resistors in series the voltage at the point between the resistors will always be the average of the voltages.
More general:
\$ V_A = \dfrac{V_1 R_2 + V_2 R_1}{R_1 + R_2} \$
so that, with \$R_1\$ = \$R_2\$ = \$R\$ we get
\$ V_A = \dfrac{V_1 R_2 + V_2 R_1}{R_1 + R_2} = \dfrac{V_1 R + V_2 R}{2R} = \dfrac{V_1 + V_2}{2} \$
How do the voltages V1 and V2 end up being added together?
By the fact that this is a linear circuit and so the superposition theorem holds.
That is, the voltage \$V_A\$ is the sum of the contributions from the voltage sources taken one at a time.
For example, zero \$V_2\$ and then \$V_A\$ is, by voltage division:
\$V_{A,V_1} = V_1 \dfrac{R_2}{R_1 + R_2} = \dfrac{V_1}{2}\$
Likewise, zero \$V_1\$ and then \$V_A\$ is, by voltage division:
\$V_{A,V_2} = V_2 \dfrac{R_1}{R_1 + R_2} = \dfrac{V_2}{2}\$
By superposition, \$V_A = V_{A,V_1} + V_{A,V_2}\ = \dfrac{V_1}{2}+ \dfrac{V_2}{2}\$
Super position is simplest.
Step 1: Ignore V2, calculate Va using V1
1/2V1 dissipation at each resistor because R1=R2 so Va = 2V-1V = 1V
Step 2: Ignore V1, calculate Va using V2
1/2V1 dissipation at each resistor because R1=R2 so Va = 3V-1.5V = 1.5V
Step 3: Super position
1V + 1.5V = 2.5V
