TEC1-12706 Peltier run from diffirent voltages

Question

My question relates to a video I saw on youtube. In this video, the user is cascading 3 TEC1-12706 peltier modules to achieve temperatures of -50 on the cold side of the cascaded peltier.

The TEC1-12706 is a 12V 6A unit, but in this video the peltiers are supplied with the following voltages as below:

Peltier 1 on the bottom - 12V

Peltier 2 in the middle - 5V

Peltier 3 on top - 3.3V

Unfortunately I don't really understand how to read the data graphs on data sheets. My question is, how does these lower voltages (5V and 3.3V) affect the performance of the TEC's, and wouldn't it be better to replace the 2 12V peltiers with a 5V and 3.3V version respectively.

EDIT

From the answer from @vindarmagnus, I left the following comment to make it more clear what I'm really after

I have an idea how cascading work, and you've confirmed what I thought. However, talking specifically about the TEC1-12706 which is a 12V module, how is its performance affected when you run it on 3.3V and 5V. Does the drop in performance justify the use of a 12V module or will it be better to get a 3.3V and 5V module instead whereby I will get better performance.

Just to add, any type of reference as to why would be highly appreciated and would also help future users

Answer 1

I have an idea how cascading work, and you've confirmed what I thought. However, talking specifically about the TEC1-12706 which is a 12V module, how is its performance affected when you run it on 3.3V and 5V. Does the drop in performance justify the use of a 12V module or will it be better to get a 3.3V and 5V module instead whereby I will get better performance.

It's hard to say without looking at the datasheets of the 3.3V\5V modules. If you wanted to choose a different module, it would need to do these things in this application:

1) Use less heat then the warmer stage below it.
2) Be more efficient than the 12V module (check the COP at an equal power for both modules)

Typically this is done by using peltiers stacks that get smaller as you get colder (to reduce power being dissipated in the modules)

The problem with peliter modules is they generate heat because they have resistance. For the TEC1-12706 you can see that they have roughly 2Ω (which varies depending on the heat load, the temperature across the module and the power being dissipated in the peltier).

In this application (where you only want to drive to a low temperature with no heat/very small heat load) and get max deltaT (temp between hot and cold side), there is a better advantage to staging peltiers with different voltages because with lower voltages each peltier generates less internal heat.

Shown below are some rough cut numbers (we don't know what the resistance of each cell is or power being dissipated so I chose 2Ω for a rough cut number, to illustrate the effect). Each stage has to move it's own heat, as well as the heat of other stages, the more heat it has to move the more it has to expend energy to do so, so using less energy down the stages gives an advantage over using 12V on all stages.

You can get an estimate of how cold any strategy will work, if we figure in the heats from the picture above we can roughly guess how cold the modules will get:

1) The 3.3V module has almost now heat load on the cold side (blue arrow) so there is rougly 20C of temperature drop (deltaT)

2) The 5V module has roughly 5-10W of heat from the module above for a 30C delta T

3) The 12V module has roughly 17-25W of heat from both modules which would be an upper bound of 40C for a deltaT

This combines for 20C+30C+40C= 90C and when we factor in ambient 25C-90C=-65C

The graph below is also for the Qc side or cold side, so the heat load calculations are done for the cold side.

Keep in mind that there is no heat load in the movie above, only heat that it is drawing from the air. If you were to put any heat load on the peltier it would reduce the stacks ability to move heat drastically as the first module would then have a heat load. There is a good app note here for designing politer modules

Answer 2

Stacking Peltier elements to achieve more heat pumping capacity is a little like bringing fuel along up in a rocket (fuel weighs down the rocket, i.e. there are diminishing returns (rocket equation)).

Peltier modules are not very efficient, and generate quite a bit of internal heat, which must be pumped away by the elements below them in the stack. This effectively lowers the throughput, although at the gain of a larger total temperature difference.

So: the 3.3 V module's gonna pump a little heat, and generate some losses. The sum of aforementioned heat and losses needs to be pumped by the 5 V module. This module in turn will generate more losses, which needs to be pumped away by the 12 V module (along with the "useful" heat transport).

Answer 3

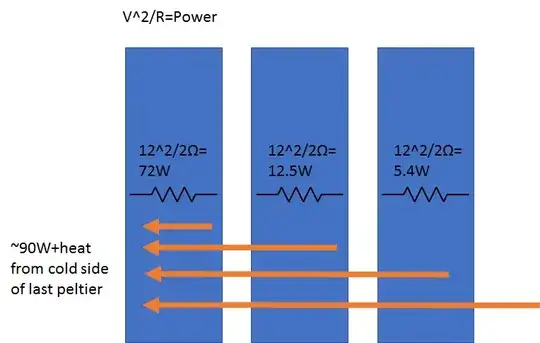
Pin = Vin × In produces -70'C drop in temp with convection warming.

Rough Schematic of 1 TEC vs 3 TECs stacked + convection vs CPU cooler

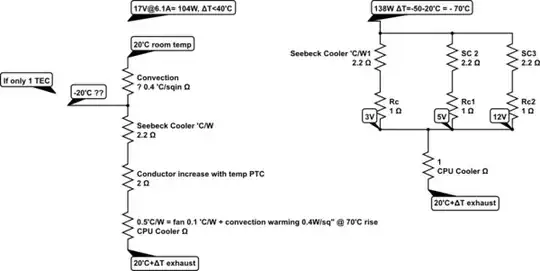
^{simulate this circuit – Schematic created using CircuitLab}

When cooling with an unknown CPU heatsink thermal resistance an equilibrium temperature is reached when the heat transferred * thermal resistance = ΔT differential temp.

With max. the cooling rate on hot side at room temp and only convection air heat load on the cold side a high temp. the differential is achieved. If the cold side was insulated, it can get much colder so the cooling area of the chip has a convection warming effect from room temp air.

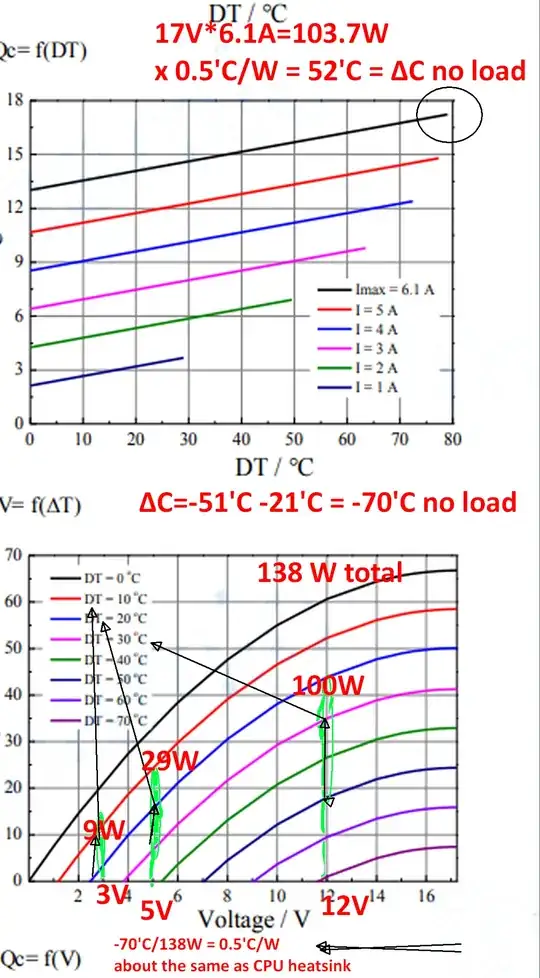
From the datasheet, I estimate a total electrical power of 138 Watts to create a ΔT of -70'C below convection air room temp on the cold side and forced air heatsink on the hot side.

This equates to 0.5'C/W which is about the same as reducing a CPU to 70'C rise above ambient or 90'C overclocking at 138 watts.

Note that even using the max voltage and current on ONE TEC you can only draw 104 Watts (103.7) and it could not achieve the same 0.5'C/W because of increased non-Peltier conductor resistance and heat loss @ 6.1A rising 3 volts or 18.3W of wasted heat from the conductor's positive temperature coefficient

However, a good question is if this cold stacked TEC were attached to the same CPU dissipating 138W and the TEC also drawing 138W the CPU could possibly operate at a 35'C rise or 55'C

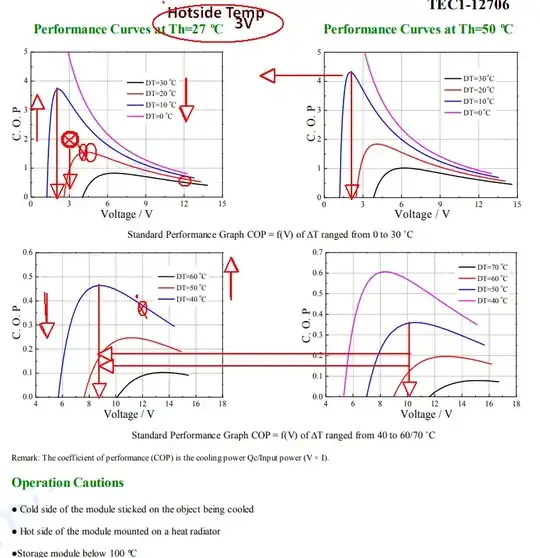
The Peltier coefficient for each hot/cold side of a module has a 4th order polynomial. SM has units [\$\frac{Volts}{°C}\$].

\$SMT_h ~or~ SMT_c = s_1T + \dfrac{s_2T}{2} + \dfrac{s_3T}{3} + \dfrac{s_4T}{4}\$

It depends on the temperature of each side and thus the difference between each side to determine the coefficient.

Yet resistive conductor losses that do not contribute to the Peltier effect increase with a 2nd order effect \$Pd=I^2R\$. When this R rises above the Peltier -ve thermal resistance, the self-heating reduces the SM coefficient. This loss is noticeable above 3V yet you need to transfer more heat to create a bigger temperature difference.

\$SM = \dfrac{(SMT_h – SMT_c) }{ DT}\$

a) The temperature difference (DT) across the module in °K or °C is:

DT = Th – Tc

b) Heat pumped (Qc) by the module in watts is:

Qc = (SM × Tc × I) – (0.5 × I2 × RM) – (KM × DT)

c) The input voltage (Vin) to the module in volts is:

Vin = (SM × DT) + (I × RM)

d) The electrical input power (Pin) to the module in watts is:

e) The heat rejected by the module (Qh) in watts is:

Qh = Pin + Qc

f) The coefficient of performance (COP) as a refrigerator is:

COP = Qc / Pin

Summary

• This COP is highest when it has perfect conductance on each side at the same temp or DT=0 .e.g. COP >5 when V+<3V which drops to 1 at 12V

• COP is lowest <<1 when very one side has very litle heat transfer on the opposite surfaces yet for stacked coolers the heat resistance is low so the temperature can drop can rise with very little heat flow.

  • COP drops to 0.1 when DT difference >40'C with higher voltage > 8V voltage rises to 12V ( less efficent at higher voltage but there is usually a peak at some lower Voltage

  

Answer 4

As others have said each peltier takes in heat on the cold side, and outputs that heat on the hot side, along with a large amount of waste heat.

Each peltier can only move a finite amount of heat (in watts) across it, while maintaining a certain temperature delta.

So lets say you start with a peltier that can maintain a 20c delta while moving 20 watts from the cold side to the hot side, and lets say it puts out double that on the hot side (made up numbers).

Stage 1 can only take in 20 watts, so we need a peltier for stage 2 that only puts out 20 watts. A simple way to do that is to just use the same peltier again, but run it at a lower voltage.

Based on these made up numbers, we would run the second stage at 50% power (by applying less voltage). The second stage would now put out 20 watts, and take in 10 watts. And now we're down 40c

Continuing this logic: stage 3 can only put out 10 watts, so we apply 25% power. Now we can take in up to 5 watts, and maintain a 60c delta.

The real numbers will vary depending on the product (probably worse). But this is the general idea.

So to answer your second question "would it be better to replace the 12v modules with 5v and 3.3v respectively". The answer is probably no. The wattage of each module is what matters. If hypothetically a 3.3v version of the peltier existed with the same wattage as the 12v version, it would not work for the 3rd stage. It would produce more heat than stage 1 and 2 could pump out, and the temperature would actually go UP.