The magnitude of the impedance of a capacitor is \$(\omega C)^{-1}\$. Plotting the impedance vs frequency should be a curve with slope \$-1/(\omega ^2C)\$. Why is it plotted as a straight line with a slope of -20dB/dec?
Thanks
A straight line with a slope of -20dB/dec IS a curve with a slope of \$\frac{1}{\omega^2 C}\$.
Think about it.
\$ 10*log_{10}(\frac{1}{\omega^2 C}) = \$ \$ -10*log_{10}(\omega^2 C) = \$
\$ -20*log_{10}(\omega) - 10*log_{10}(C)) \$
A Bode plot is in a linear dB scale in the ordinate and logarithmic scale in the abscissa.
Because we always plot the magnitude, an not the coplex impedance. If you take the magnitude of \$(j\omega C)^{-1}\$ you get \$(\omega C)^{-1}\$
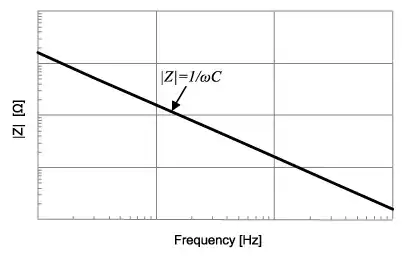
Source: https://www.murata.com/en-us/products/emiconfun/capacitor/2013/02/14/en-20130214-p1
dBunits is proportional to thelogof the "plain" value. Try it out. – Eugene Sh. Mar 07 '19 at 20:46log(1/x) = log(1)-log(x). But yourxis is gaining power of 10 every "tick", solog(x)will have a constant step every tick. – Eugene Sh. Mar 07 '19 at 20:52