Consider the following
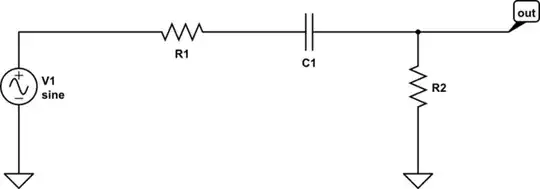
simulate this circuit – Schematic created using CircuitLab
$$ H(s) = \frac{sR_2C_1}{1+s(R_1+R_2)C_1}$$ $$ f_z = \frac{1}{2\pi R_2C_1} $$ $$ f_p = \frac{1}{2\pi (R_1+R_2)C_1} $$
I simulated the circuit in LTSPICE with \$R_1=R_2=795\$ and \$C_1=1nF\$ which should give me a \$f_z = 200kHz\$ and \$f_p = 100kHz\$.
Here is the AC anaylsis of the simulation.
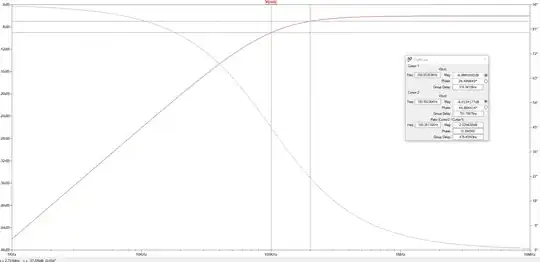
Question: Given that there is a zero at the origin with a certain frequency - what should I see at that frequency ?
Additional information to add some clarity: I am reading this book about Linear Circuits and it says the following
$$ H(s) = \frac{sR_2C_1}{1+s(R_1+R_2)C_1} = \frac{\frac{s}{w_{z0}}}{1+\frac{s}{w_{p1}}} $$
where \$ w_{z0} = \frac{1}{R_2C_1} \$ and \$ w_{p1}= \frac{1}{(R_1+R_2)C_1} \$
I believe the intent of this form is to visually be able to extract certain information about the system. I am confused on the significance of the \$w_{z0} \$ and what it means.
Traditionally I have seen forms such as $$ H(s) = \frac{1+\frac{s}{w_z}}{1+\frac{s}{w_p}}$$ and I know that you have a flat line (magnitude plot) until the wz and then you have an +20db/dec line and then a -20db/dec at the wp. But this zero at the origin is messing me up.