In large signal analysis of differential amplifier there are some equations to determine iDS.
If we simplify it looks like that :
\$ \large 2x^2+2kx+k^2-2\frac{l}{m}=o\$
Is there an easy way to solve these kind of equations. What should one study to easily solve these kind of problems?
Edit
Original equation looks like this.
Citation :
Agarwal, Anant, Lang, Jeffrey. Foundations of Analog and Digital Electronic Circuits.. [edx].
Edit
Ok. I solved equation using completing the square technic.
\$ \large (x+\frac{k}{2})^2 = \frac {l} {m} - \frac{k^2}{4}\$
\$ \large x = \frac{1}{2}(\frac {\sqrt {4l-mk^2}}{\sqrt{m}} - k) \$
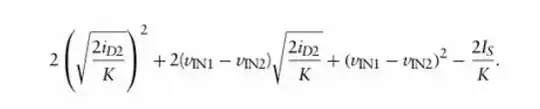
xis the unknown). Grade 6 or so.... – Eugene Sh. Mar 27 '19 at 15:07