How to estimate a linear power supply efficiency in LTspice?

Question

I have a little transformer that I would like to turn into a 5V power supply. Before building it I decided to model the device in LTspice:

The inductance of the primary and secondary windings were measured using an LCR-meter. The wave on the output 20 Vpp in LTspice agrees with what I see on the oscilloscope. The linear voltage regulator is not shown. Since V(OUT) is 5.6-8.5V I would like to use L4941 LDO which has maximum 0.6V drop. But I couldn't find a model for it.

What bothers me is that calculated efficiency is about 8%:

pin: AVG(abs(v(in,ingnd)*i(v1)))=5.46445 FROM 0 TO 500
pout: AVG(5*i(i1))=0.45 FROM 0 TO 500
eff: pout/pin=0.0823504

What brings a question - is such low efficiency expected for such a simple power supply? Maybe I'm calculating it the wrong way? Or there is something wrong with the design itself? I've uploaded the model here.

UPD: After replacing diodes with 1N5408 and C1 - with 1200 uF capacitor I could increase the current through D1-D4 to 3A and the load current to 500 mA. This gives an efficiency about 35.6%. Still it doesn't look right.

Answer 1

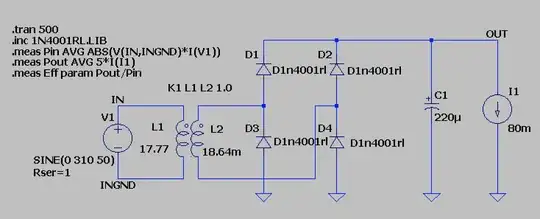
I'm surprised it works, there is no reference to ground on the primary side. At the very least -- if you intend to have the primary "floating" -- add a resistance of (say) 1 Meg to ground from one of the nodes. Also, for measurements, you're better off imposing a timestep and reducing the enormous timespan, e.g. .tran 0 100 90 1m, and disabling waveform compression with opt plotwinsize=0.

About the efficiency, what you have there is an 18 H primary which is very large compared to the current. If you plot the current vs the voltage across the primary you'll see that they're almost 90^o displaced. That makes for very small efficiency. You would also have some Ω DC resistance (more than 1 Ω), most likely, which will also contribute to the damping.

You also have an unadulterated diode bridge, and that is strongly nonlinear, it generates a lot of harmonics, and those tend to bury the fundamental. See this for a more detailed explanation.

In short, you have mostly the magnetizing current and the severely displaced fundamental + attenuated harmonics mostly due to the large value of the primary inductance (which helps with filtering but adds extra displacement).

---

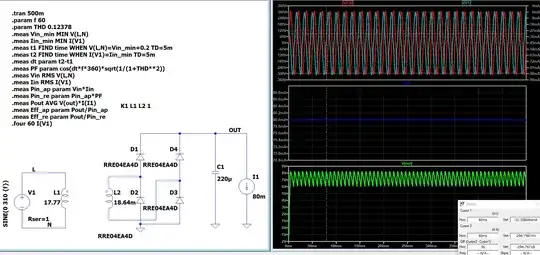
You are calculating the powers completely wrong. For the output power you are using 5*I(I1), which means you are assuming 5 V output while explicitly writing I(I1), which can be simply replaced by 90m. For the input power, it's not the average of the absolute values, it's simply the average of the product of the input quantities. This means that your results are unreliable. Here is a remade version:

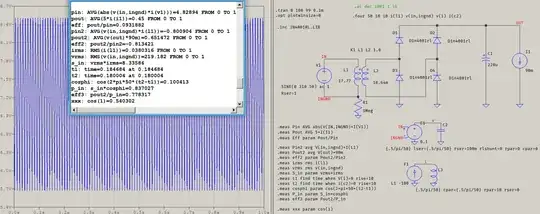
The output voltage is ~7.24 V average (plotted), so now the output power is Pout2 in the error log. Also, Pin2 is different.

@vtolentino's way of measuring is a bit misleading because it implies measuring the displacement factor, but that applies to the fundamental, only, and the current has harmonics. Even then, a better way of measuring would be using a bandpass (F1 and L3), which has zero phase at f0. To balance the possible phase delays, E1 and C2 apply the same filtering to the voltage, even if this is a bit useless here since the difference in phase is about 0.05^o. Still, that's how I measured it.

The difference between calculations is shown in the error log: vrms and irms being the input RMS values, and cosphi being the attempted measurement of the displacement. Using that to calculate the power as vrms*irms*cosphi results in a different efficiency, eff3=77.83%, compared to eff2=81.34% (negative because I(L1) goes into V1, not out of; same thing) It's not much of a difference, true, but it matters.

That last measurement is to show that I have checked the Use radian measure in waveform expressions in the Control Panel > Waveforms, by default unchecked, that's why I am using cos(2*pi...) instead of cos(360...). Also, that 1 Meg resistor is there for .AC analysis, that fails without it; .TRAN can live without it.

The first part of the answer remains valid, though, partly because the part about harmonics and magnetizing inductance influences what results you see in the picture above, and partly because it does affect the way the apparent power is calculated, even if not needed here.

Answer 2

You are basically facing a Power Factor Correction problem when you are measuring the input power. Since there is some lag between the phase and voltage, the measured input power (apparent power) is not exactly the power which is being delivered to the rest of the circuit. This happens when you are driving an inductive load (transformer) and/or a capacitive load (filter capacitor) with an AC source. In order to evaluate the effective power being drawn from the source, you would have to measure the real power:

$$P_{REAL} = PF \cdot P_{APPARENT}$$

where:

\$PF\$ is the power factor and defined as \$PF=\cos \theta\ \cdot \left(\dfrac{1}{1+THD}\right)^{0.5}\$

\$\theta\$ is the phase difference between the supplied voltage and current.

\$THD\$ is a total harmonic distortion. In the case of pure sinusoidal source it is zero.

I could think of two approaches you could use:

1. run the simulation, and measure the phase difference of the waveforms. Run an FFTand measure the THD for the frequency of interest. Calculate the power factor and then work out the effective input power.
2. Parametrize everything and try to measure the phase difference between two signals (a bit tricky I must say, to determine where to select the phase). I tried the following simulation, and apparently it works fine, but you would need some fine tuning for your final application. As for the THD, it can be obtained in a first simulation through the command .four 60 I(v1)

For this simulation, I obtained an efficiency of \$4.7\%\$ when using the apparent power (wrong) and an efficiency of \$62.9\%\$ when using the real power, which sounds much more realistic.

Answer 3

The problem is in the formula you used for measuring power in,

AVG(ABS(V(in,ingnd)*I(v1)))

As the voltage and current are out of phase, power goes negative at times when the voltage and current have opposite signs. Therefore you should not apply the ABS function, but simply average all the instantaneous power values (both positive and negative).

After changing the formula to AVG(V(in,ingnd)*I(v1)), power in is reported as 0.804 W and efficiency (with output regulated to 5 V) is 56%.

Another way to show power in LTspice is to hold down Alt while clicking on a component (which produces a trace of instantaneous power in it) then hold down Ctrl and click on the trace label to show the ave rage power.

When we do this to I1 we see that the output power is not 0.45 W but 0.653 W, indicating a circuit efficiency of 0.653/0.804 = 81%. The difference is the loss in your 5 volt linear regulator.

However this is not an accurate simulation because you have not included transformer winding resistances. Using the measured values you reported in the comments (primary 1.4 KΩ, secondary 3 Ω) the circuit efficiency drops to 23% without regulation to 5 V, and 18% with it.