2

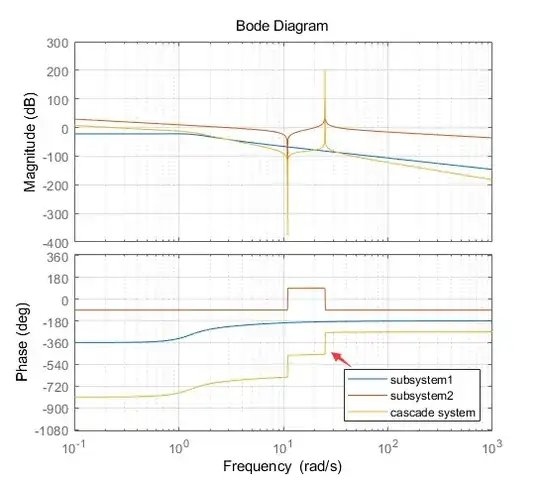
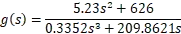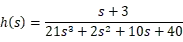I have two subsystems which the transfer functions you could see below as g(s) and h(s). According to some references show below, I found that the bode plot of a cascade system should be the sum of subsystems. Then, to comfirm that I implemented code as below in Matlab, but the result seems violate with the reference. So, where I went wrong?

Subsystem transfer functions:

enter image description here

enter image description here

Matlab code:

den = [0.3352 0 209.8621 0];
gs = tf(num, den);

num = [1 3];
den = [21 2 10 40];
hs = tf(num, den);


c = gs*hs;


figure
bode(hs,gs,c)
grid on
legend('subsystem1','subsystem2','cascade system')

Result:

enter image description here

Reference:

Fig1

user5558685
  • 23
  • 2
  • "bode plot of a cascade system should be the sum of subsystems". When gain is in dB. Is your question about gain or phase addition? – AJN Sep 11 '20 at 04:54
  • In the plots, the phase is not restricted to either (+0, +360) or (-180, +180). That may be why it doesn't look like addition. If it is matlab, right click to get to properties window and deselect unwarp phase option and check again. – AJN Sep 11 '20 at 04:57

1 Answers1

1

If your question is about the phase plot, then note that 0deg phase is same as 360deg phase. You can add or subtract multiples of 360 deg to phase diagram without changing the physical meaning (conditions apply).

In the plots, the phase is not restricted to either (+0, +360) or (-180, +180). That may be why it doesn't look like addition. If it is matlab, right click to get to properties window and deselect unwrap phase option and check again.

AJN
  • 3,831
  • 1
  • 10
  • 20
  • Thanks AJN. Could you give me some detailed information or references about "(conditions apply)" you just told? – user5558685 Sep 11 '20 at 06:29
  • For steady state analysis you can add or subtract 360 deg multiples without problems. But if you try to convert the phase delay to time delay (for a specific frequency) using $delay = \angle / \omega\ \ (\text{rad / (rad/s)})$ and apply it to transient conditions, restricting the phase value may lead to surprises. I'm not sure though. That is why I added the caution. – AJN Sep 11 '20 at 06:46