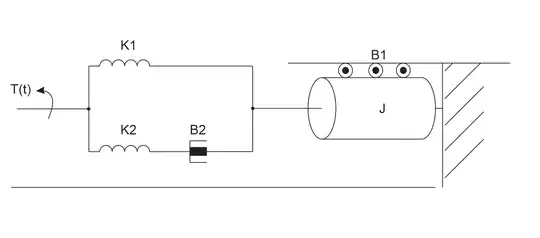
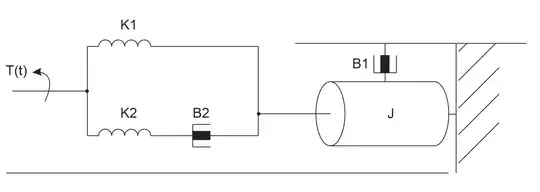
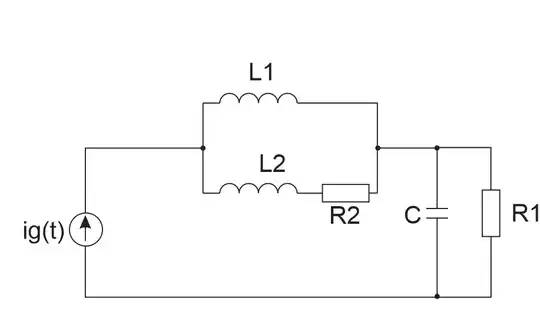
So I practiced various examples of modeling electrical cricuits and mehanical circuits. I stumbled upon this one:
now with these direct substitutions: $$k=\frac{1}{L},\;B=\frac{1}{R},\;J=C,\;T_{(t)}=i_{g(t)}$$ I get these equations: $$i_g=i_{l1}+i_{l2}$$ $$i_{R2}=i_{l2}$$ $$i_c=(i_{R2}+i_{l1})-i_{R1}$$
Now, which number of independent energy-storage elements is in this circuit? Which order is differential equation which describes this circuit and how it looks like? I got this: $$i_{g(t)}=i c+i_{R1}=C \cdot \frac{d uc}{d t}+i_{R1}=C \cdot \frac{d u_c}{d t}+\frac{uc}{R{1}}$$ Is this differential equation which describes this circuit?