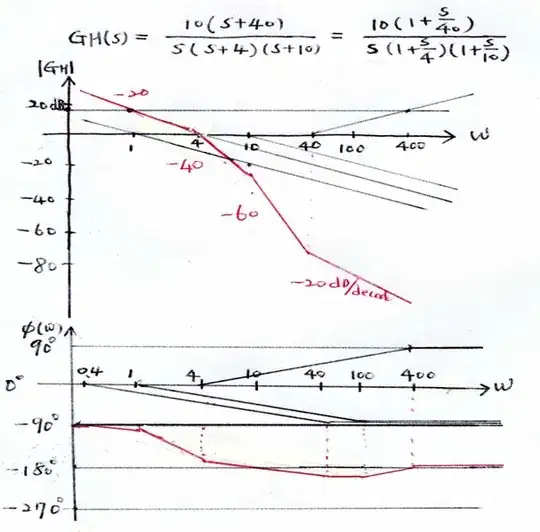
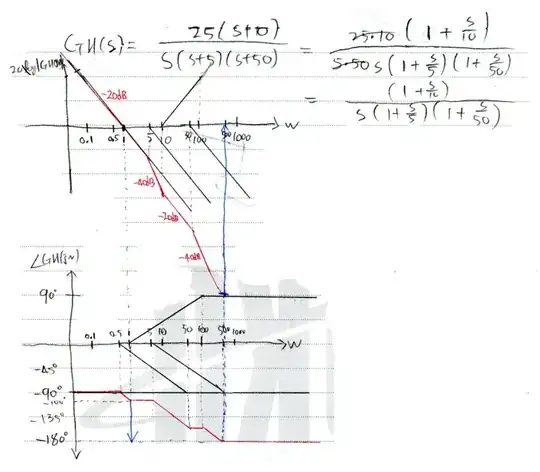
How do I get the slope and intersection point?
Start with a very simple example: -
$$H(s) = \dfrac{1}{s}$$
When \$s = 1\$, the amplitude of the transfer function is clearly 1.
When \$s = 0.1\$, the amplitude is 10.
When \$s = 10\$, the amplitude is 0.1.
If you convert those amplitudes to dB you would have: -
- When \$s = 0.1\$, gain = 20 dB
- When \$s = 1\$, gain = 0 dB
- When \$s = 10\$, gain = -20 dB
So, immediately you can see that if s increases by 10 the gain falls by 20 dB. This is why we call the slope -20 dB/decade: -
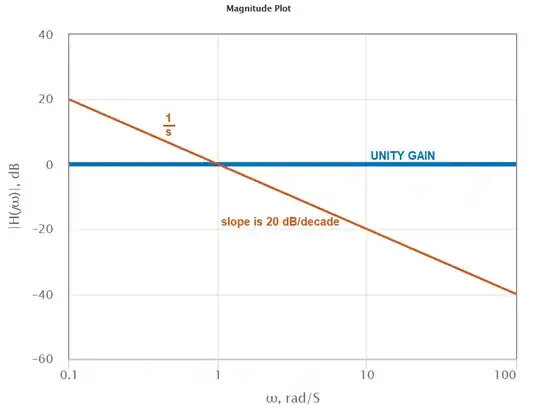
It's a little bit different with this: -
$$H(s) = \dfrac{1}{s + 1}$$
- When \$s = 0\$, the gain is 1 (this is a DC gain of 1)
- When \$s \neq 0\$ we have to remember that s has a complex value so, if \$s = 0.1\$, the transfer function becomes this: -
$$H(s) = \dfrac{1}{j0.1 + 1}$$
And, to solve that for gain magnitude we add the square of the terms in the denominator and take the square root like this: -
$$|H(s)| = \dfrac{1}{\sqrt{0.1^2 + 1^2}} \approx \dfrac{1}{1.005} \approx 1$$
Notice that we made an approximation here.
The impact of that approximation is that we say gain is flat from DC up to at least \$s = 0.1\$. If we then made \$s = 1\$ we get this: -
$$|H(s)| = \dfrac{1}{\sqrt{1^2 + 1^2}} = \dfrac{1}{\sqrt2} = 0.7071 = \text{-3 dB point}$$
For this particular equation (\$\frac{1}{s+1}\$), when \$s = 1\$ we are at the 3 dB point.
This is because 20 log(0.7071) = -3.01 dB. We call it the 3 dB point loosely but it's really the -3 dB point (get used to it!).
However, because we are wanting to sketch a frequency response from the H(s) formula, we don't mind a diagram error of 3 dB and so, we say when sketching it, that the transfer function is flat from DC all the way to \$s = 1\$.
We can draw a straight line on the bode plot at 0 dB from a very low frequency to the frequency where \$s = 1\$. Above that frequency at (say) \$s = 10\$, the gain magnitude is: -
$$|H(s)| = \dfrac{1}{\sqrt{10^2 + 1^2}} = \dfrac{1}{\sqrt{101}}$$
This is a gain magnitude of 0.0995 or about -20 db.
So then we draw another straight line falling from 0 dB at \$s = 1\$ to -20 dB at \$s = 10\$. The line (red) will clearly continue falling at 20 dB per decade hence it continues to -40 dB at s = 100: -
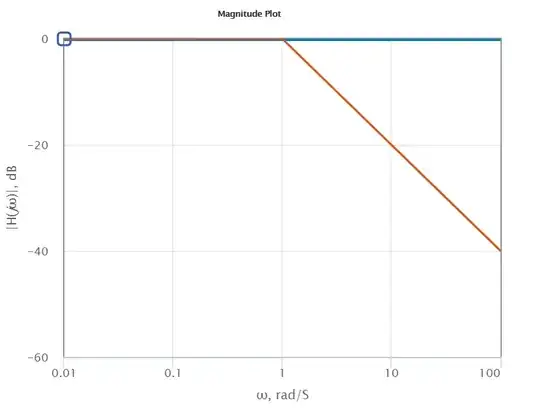
Image above from this website and you can put your own numbers into the page and get your own specific results. It even provides you the phase angle plots.
Here's what your actual transfer function is on the page above: -

And it results in this magnitude plot: -
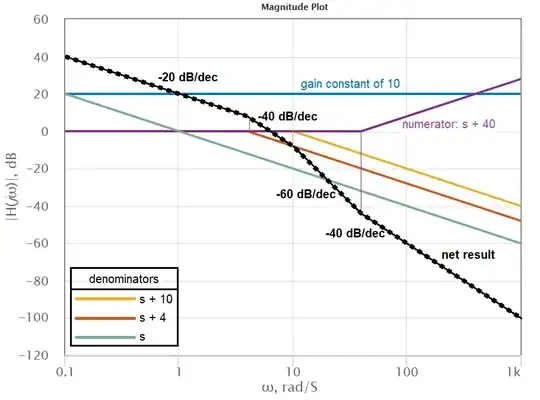
I think you should be able to manage this from now?