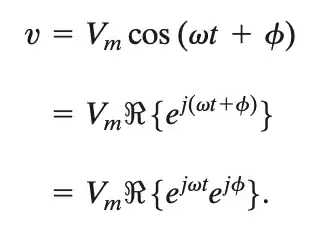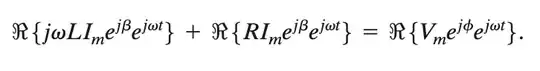So reading chapter 9 in James W. Nilsson, Susan Riedel-Electric Circuits (10th Edition) book explains perfectly how can complex numbers be used to add and subtract sinusoidal waves as in the below figures:
due to the property that adding the real parts of any two complex numbers is equivalent to adding the complex numbers as a whole and getting the real part of the result which is very intuitive and makes sense, however this is not true for multiplication or division(multiplying the real parts of two complex numbers is not equivalent to multiplying the complex numbers as a whole and getting the real part of the result), which makes me wonder how can Ohm's law for AC Circuits (V = I*Z) be possible using complex numbers to get the voltage by multiplying together the impedance and current where both are complex numbers.