-1

I would like to model a 10 meter twisted pair wire from a CAT 6 ethernet cable. I'm trying this out so that I can know if my driver circuit is capable of sending a signal that is still acceptable for the circuit on the other end.

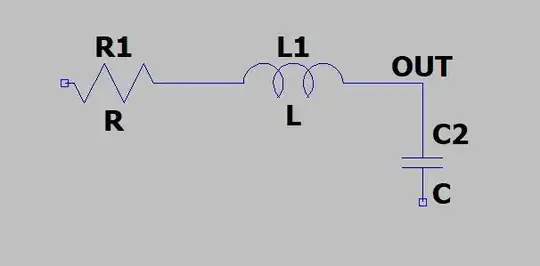
enter image description here

Is this correct? What is correct way for getting the values? Resistance seems to be the easiest, I took a multimeter and measured a 10 meter UTP which showed a value of 0.8 ohms. I have read according to this article that the worst allowable resistance for a CAT 6 is 2 ohms per 10 meters, so I will be assuming that.

That is all I can possibly think of getting with my measly multimeter. How about inductance and capacitance? According to this nominal capacitance is 46 pF/m so do I just multiply that by 10 and I have my capacitance?

The signal is a 800 kHz 1-wire digital signal. What would be the best to place on the other wire of the twisted pair? Ground? 5 V? Floating?

winny
  • 14,707
  • 6
  • 46
  • 66
DrakeJest
  • 887
  • 11
  • 39
  • 1
    Twisted pair cabling for ethernet acts as a 100 ohm transmission line - it cannot be simulated using lumped parameters. 800kHz is very low - the cable is designed for hundreds of MHz. – Kevin White Sep 29 '21 at 18:09
  • https://electronics.stackexchange.com/q/181590/82111 does this help? – Marko Buršič Sep 29 '21 at 18:12
  • 1
    LTSpice has transmission line models. You'll have to fill in some of the parameters for your specific set of wires. https://ez.analog.com/design-tools-and-calculators/ltspice/f/q-a/545102/transmission-line-in-ltspice – Aaron Sep 29 '21 at 18:13
  • @MarkoBuršič it looks like i still need the L(inductance) and C(capacitance) values. – DrakeJest Sep 29 '21 at 18:21
  • @Aaron looks like the transmission line model still needs the RLC values, i have no idea what are the correct values for the L and C. – DrakeJest Sep 29 '21 at 18:25
  • 3
    Don't use L and C, use a 100 ohm transmission line model. If you must use a ladder of Ls and Cs, then compute the values from the 100 ohm impedance of the line using the Telegrapher's Equation (wikipedia). You'll have to device how many sections to use, 10, 20 perhaps. It's far easier just to use the transmssion line model directly – Neil_UK Sep 29 '21 at 18:34
  • https://en.wikipedia.org/wiki/Category_5_cable#Characteristics – Aaron Sep 29 '21 at 18:40
  • 1
    What's the point of simulating a transmission line without knowing the parameters? – Marko Buršič Sep 29 '21 at 19:00
  • What should I do when someone answers my question? – Andy aka Dec 13 '22 at 12:38

2 Answers2

2

The CAT6 has a characteristics impedance of 100 ohm

$$Z_k=\sqrt{\dfrac{j\omega L + R}{j\omega C + G}}$$

At higher frequency the reactive component is much greater than resistance and conductance so the simplified version is:

$$Z_k=\sqrt{\dfrac{L}{C}} = 100\Omega$$

Any line with the same L/C ratio also has the same characteristics impedance, but the L and C may be different from one to another.

enter image description here

You can use lossless transmission line in LTspice - tline

$$T_d=\dfrac{l}{v}=\dfrac{l}{c\cdot k_v}$$

Better you could use a lossy transmission line - ltline, if you for example derive the L from known C.

enter image description here

Marko Buršič
  • 23,961
  • 2
  • 20
  • 33
1

looks like the transmission line model still needs the RLC values

If you know the capacitance per metre value then you can calculate inductance per metre using this formula: -

$$Z_0 = \sqrt{\dfrac{L}{C}}$$

Where \$Z_0\$ is the characteristic impedance of the cable (circa 100 ohms).

Then, given your maximum frequency of interest you can decide to model the line as several lumped networks of R, L and C where each represents a short length of cable. That short length will be decided by the maximum operating frequency (including relevant harmonics). So, if you were interested in a maximum frequency of (say) 300 MHz, the wavelength is exactly 1 metre in air and about two thirds of a metre in a cable. Why two-thirds: -

Velocity of propagation is the speed at which an electrical signal travels through anything and equals: -

$$V_p = \dfrac{1}{\sqrt{L\cdot C}}$$

Where \$L\$ and \$C\$ are the inductance and capacitance per unit length of the cable hence, for a typical 50 Ω cable having 250 nH/m and 100 pF/m, \$V_p\$ equals 200,000,000 metres per second (do the math!) and this is two thirds the speed of light.

You would then model each section as equivalent to one tenth of a wavelength long i.e. each section would be physically representative of 6.6 cm.

Or just calculate L and use the transmission line model in your simulator.

Andy aka
  • 456,226
  • 28
  • 367
  • 807