why is the equation on the left equals the right?
know would I derive it?
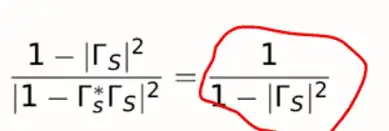
Asked
Active
Viewed 63 times
2 Answers
2
It's just that \$\Gamma_S^* \Gamma_S = \lvert \Gamma_S \rvert^2\$. Thus $$ \frac{1 - \lvert \Gamma_S \rvert^2}{\lvert 1 - \Gamma_S^*\Gamma_S \rvert^2} = \frac{1 - \lvert \Gamma_S \rvert^2}{( 1 - \lvert \Gamma_S \rvert^2 )^2} = \frac{1}{1 - \lvert \Gamma_S \rvert^2}, $$ as desired.
Keeley Hoek
- 287
- 1
- 9
1
Some guidance:
A complex number multiplied by its conjugate is the square of the absolute value.
See it (a+bj)(a-bj)=a^2 - abj + abj - (bj)^2 = a^2 + b^2 = the square of the absolute value of a+bj (only remember that j^2 = -1).