Determining currents in each part of the circuit using Kirchhoff 's laws

Question

During this question I have applied the junction rule and the loop rule but I am stuck on the next stage:

I₁ = I₂ + I₃

Loop 1 and 2 will be both in the clockwise direction.

Loop 1:
30 - 8·I₁ - 6·I₂ = 0

Loop 2:
-3·I₃ + 6·I₂ = 0

Now here I am unsure on the next step; do I simplify the expressions given, or sub in I₁ = I₂ + I₃ into the first loop replacing I₁ in 8 or do I use simultaneous equations by substitution or using matrix algebra?

Answer 1

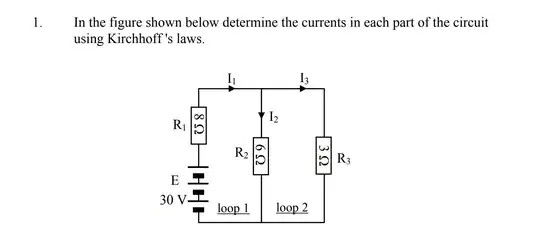
Your equations look correct to me. Congratulations on keeping resistor voltage polarities consistent with current direction labels, that's usually where people mess up. Your question, though, is not an electrical question, it's a maths question.

You have three unknowns, \$I_1\$, \$I_2\$ and \$I_3\$, and three independent equations relating them, which means they have a solution.

You may use any technique you choose for finding \$I_1\$, \$I_2\$ and \$I_3\$, including matrix manipulation, and including variable substitution. They will all yield the same results, since the underlying algebraic principles of these techniques are fundamentally identical.

I suggest you try both approaches, and prove to yourself that they yield the same results.

Solution by matrices

To tackle this problem using matrices you first need to arrange your equations:

$$ \begin{aligned} I_1&& -I_2&& -I_3&& =&& 0&& \\ \\ -8I_1&& -6I_2&& && =&& -30&& \\ \\ && 6I_2&& -3I_3&& =&& 0&& \\ \\ \end{aligned} $$

This structures the coefficients of each variable in a manner that permits you to construct the matrix equation:

$$ \begin{bmatrix} 1 & -1& -1 \\ -8 & -6 & 0 \\ 0 & 6 & -3 \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} = \begin{bmatrix} 0 \\ -30 \\ 0 \end{bmatrix} $$

From there, either you perform row manipulations to arrive at a solution, or you find the inverse of this left matrix, and the solution falls out:

$$ \begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} = \begin{bmatrix} 1 & -1& -1 \\ -8 & -6 & 0 \\ 0 & 6 & -3 \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ -30 \\ 0 \end{bmatrix} = \begin{bmatrix} 3 \\ 1 \\ 2 \end{bmatrix} $$

Solution by substitution

If you do substitute \$I_1=I_2+I_3\$ into the KVL equations, you reduce the problem to two simultaneous equations:

$$ \begin{aligned} -14I_2&& - 8I_3&& =&& -30 \\ \\ 6I_2&& - 3I_3&& =&& 0 \\ \\ \end{aligned} $$

Again, what you do with this is up to you, but I will perform another substitution in an attempt to eliminate \$I_3\$. Rearranging the second equation:

$$ \begin{aligned} 6I_2 - 3I_3 &= 0 \\ \\ 3I_3 &= 6I_2 \\ \\ I_3 &= 2I_2 \\ \\ \end{aligned} $$

A final substitution will reveal \$I_2\$

$$ \begin{aligned} -14I_2 - 8(2I_2) &= -30 \\ \\ -30I_2 &= -30 \\ \\ I_2 &= 1 \end{aligned} $$

Therefore:

$$ \begin{aligned} I_3 &= 2I_2 \\ \\ &= 2 \\ \\ I_1 &= I_2 + I_3 \\ \\ &= 3 \end{aligned} $$

As you can see, the solution by substitution agrees with the matrix solution.

Verification by element composition

If I'm honest with you, I wasn't sure about these prior solutions, so I just did a quick simplification of your circuit, which is easy when you notice that \$R_2\$ and \$R_3\$ are in parallel. By composing a single resistance \$R_{23}\$ from that pair, verification of my calculation of \$I_1\$ is trivial:

$$ R_{23} = R_2 \parallel R_3 = \frac{R_2 \times R_3}{R_2 + R_3} = \frac{18}{9} = 2\Omega $$

\$R_{23}\$ is in series with \$R_1\$, so we can combine them into a single resistance \$R_{123}\$:

$$ R_{123} = R_1 + R_{23} = 10\Omega $$

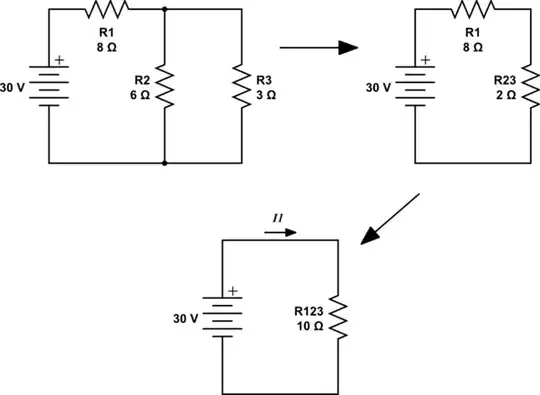
^{simulate this circuit – Schematic created using CircuitLab}

A quick application of Ohm's law reveals \$I_1\$:

$$ I_1 = \frac{30V}{10\Omega} = 3A $$

Now I'm convinced that the value I derived above for \$I_3\$ is correct.

By inspection I can see that since \$R_2\$ and \$R_3\$ are in parallel, then the voltage across them must be the same. The current through them must therefore be (inversely) related by their resistances. Without doing any maths, I can tell straight away that the current \$I_2\$ through 6Ω must be half of the current \$I_3\$ through 3Ω.

Knowing the sum of these currents to be \$3A\$, in my head I can work out that \$I_2=1A\$ and \$I_3=2A\$, which all agrees with the values I found before, using less inuitive approaches.

Conclusion

The answer to your question is: You can use any method you like to attack this problem. You may obtain equations from Ohm's and Kirchhoff's laws, and solve the resulting simultaneous equations either by substitution or by any matrix technique. Or, in many cases, you may use component composition to simplify circuits, and apply Ohm's law alone to reveal circuit state.

The results of all these techniques must necessarily agree with each other, since at their heart they are all describing the system using the same underlying algebraic principles.

Answer 2

\$I_1=I_2+I_3\$

is correct.

I don't even bother defining that the way you did. I just have a big loop of \$I_1\$ and a big loop of \$I_2\$. Then when tracing out voltage drops along the loop, if I encounter a component with more than one current in it, I write down the current expression as the sum or the difference between the two directly. \$I_1\$ and \$I_3\$ already encompass the entire circuit so introducing \$I_2\$ is just a redundancy you need to keep track of.

---

You seem to be having trouble knowing which polarity to write the voltage drops as in your loop equations. We use the passive sign convention which means that positive = voltage drop (a load) and negative = voltage rise (a source).

In other words, when tracing the voltage drops along a loop if you go from - to + through the component, that is a negative voltage drop (a voltage rise) which means it is a source. Conversely, if you go from + to - through the component then that is a positive voltage drop (just a voltage drop).

Then when you encounter something that does not have + or - labelled (such as a resistor of unknown voltage drop), you assume that the direction you defined your current loop to be correct and you assume that the unknown device is a load. That means you define the polarity of the unknown voltage drop to be + on the terminal you enter and - on the terminal you exit when tracing the voltage drop. If your assumed wrong, then your calculated loop current will simply be a negative value and if the unknown load ended up actually being a source then it will simply return a negative voltage value. All that it means is that your guess was wrong. Positive = your quess was correct. Negative = your guess was wrong.

Therefore for loop 1,

\$30-8I_1-6I_2=0\$

should be:

\$-30 + 8I_1 + 6I_2 = 0\$

Similarly, for loop 2

\$-3I_3+6I_2=0\$

should be \$3I_3-6I_2=0\$

Mathematically equivalent, yes, but if using passive sign convention then that is the way they should be initially written when you first formulate them because if you don't it's going to cause you issues in more complicated circuits and loops. You can the manipulate them afterwards.

Answer 3

You are using KCL for the top node but I dont see Node voltage analysis instead you are using Mesh current analysis and this is where problems start to be appeared.

As DKNguygen has already pointed out I1 is the current of the mesh of the voltage source and I3 is the current of the mesh of the 3Ω resistor.I2 is the net current flowing inside the 6Ω resistor.But I1 is not equal to I2+I3 because now you are working with meshes , not nodes.