Differential amplifier current source problem

Question

I got this question on my exam:

Assume the two input voltages \$v^+\$ and \$v^-\$ are equal such that \$v^+=v^-=v\$, and the two transistors Q1 and Q2 are identical. What is the lowest value for \$v\$ before the current source breaks down?

Eg. if \$v=V^-\$, there will be no current through the transistors which contradicts the current source \$ I_0 \$. With a higher \$v\$ the transistors will start to conduct, and there will no longer be a contradiction, but at what value of \$v\$ does this happen?

In the original question, the current source \$I_0\$ was an ideal current source, like in picture a), which of course never breaks down. Let's instead assume that the current source is implemented with a mosfet like in picture b). This transistor has a gate voltage \$V_{ref}\$ set so that the drain current is relatively constant assuming it's in the saturation region. In this case, I guess the question boils down to what is the minimal value of \$v\$ while the current source transistor still is in the saturation region.

Answer 1

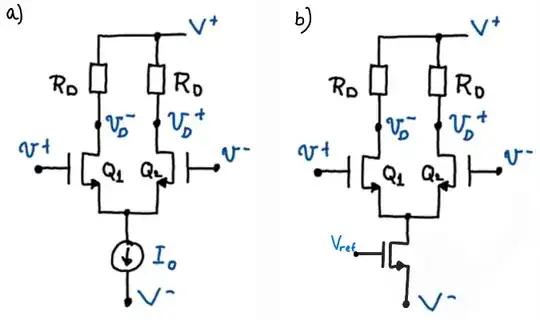
This is a fairly typical analysis of headroom, so I'll give an overview that you can apply to this problem and generalize to other problems. Since this is a study/practice question, I will hold off on giving the exact answer to give you an opportunity to work through all of the steps and apply the remarks I gave.

First, we assume that all transistors must remain in saturation, and must be in neither cutoff nor triode. For this amplifier which operates purely linearly, it's a good assumption - indeed, the amplifier relies on the current source being a solid current source, which only happens during saturation, and gain only results from Q1 and Q2 acting as good transconductors (again, during saturation).

As a second simplifying assumption that follows from assuming saturation, we can assume that the current remains close to the nominal current - i.e. the bottom transistor drain current is \$I_0\$ and Q1/Q2 each have a drain current of \$I_0/2\$.

This now gives us another simplifying assumption - the Vgs of each transistor is close to the nominal Vgs at the desired operating point. This is true because the current is close to nominal, and the transistor is in saturation, i.e. square-law.

We wish to work with the common-mode voltage applied to the gates of Q1 and Q2 - you called it \$v\$, but I'll call it \$V_{CM}\$ to distinguish it from other voltages. It should follow that the source of Q1/Q2 is one Vgs drop below \$V_{CM}\$ if Q1/Q2 are in saturation.

Finally, we now need to ensure that the bottom transistor is in saturation as well. According to this nice reference sheet from UC Berkeley, the condition for saturation is that \$V_{GS} > V_T\$ (assumed true already, since the mirror is biased) and \$V_{DS} > (V_{GS} - V_T)\$. In some derivations, you may see some people refer to \$(V_{GS} - V_T)\$ as \$V_{ov}\$ (i.e. the overdrive voltage).

Finally, the source of Q1/Q2 is the drain of the bottom transistor, so by knowing the voltage at that node from before, you know \$V_{DS}\$. You can now use that with the \$V_{DS} > (V_{GS} - V_T)\$ condition to figure out the minimum allowable value of \$V_{cm}\$.

Ultimately, you should obtain a formula in terms of the V- supply rail voltage, Vgs of Q1/Q2, Vref, and Vt of the bottom FET. If you know the actual numerical parameters of the FETs, you can go further and calculate a numerical answer.

For a more complex circuit, you can do the same analysis, step by step in the chain, and generalize this technique.