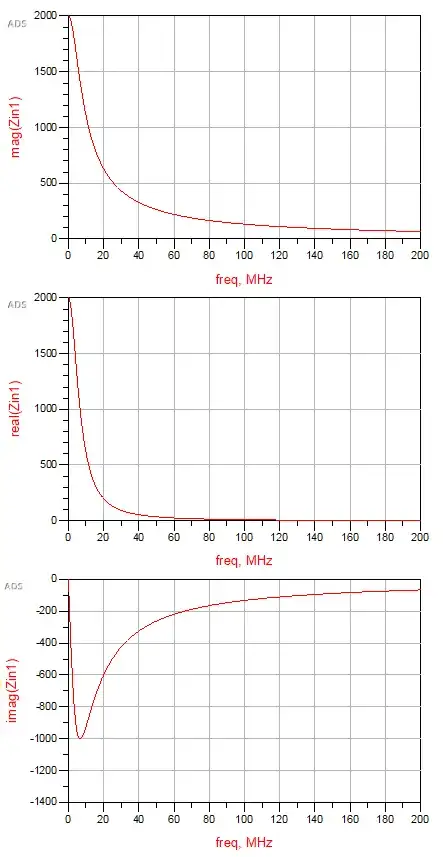
Why doesn't the real part of the impedance always equal to the
resistor in an ideal parallel RC circuit?
- A complex impedance is specified in this format: \$a+jb\$.
- This represents two series components, one resistive (\$a\$) and one reactive (\$b\$)
- Your circuit is a parallel arrangement and this necessitates conversion to series values
- This inevitably produces values that are frequency dependent
- It's easy enough to see at DC and infinite frequency
My question is that why the real part of the impedance changes with
frequency, the real part represents the resistive part of the complex
impedance right?
You should be able to see that now: -
- At DC the real part is 2 kΩ but,
- At infinite frequency, the real part is 0 Ω.
If you want the math, just convert the parallel R and C into an impedance: -
$$Z = \dfrac{R\cdot\frac{1}{j\omega C}}{R + \frac{1}{j\omega C}}\rightarrow \dfrac{R}{1+j\omega CR}$$
Multiply top and bottom by the complex conjugate of the denominator to get this: -
$$\dfrac{R\cdot (1-j\omega CR)}{1+\omega^2C^2R^2}$$
This makes the real part (\$R_{SERIES}\$) equal to: -
$$\dfrac{R}{1+\omega^2C^2R^2}$$
And \$R_{SERIES}\$ is clearly frequency dependent.