The following is my analysis.
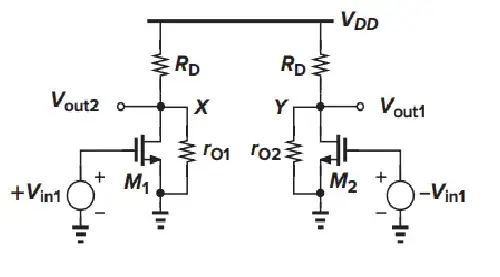
Firstly, we analyse the left part of this circuit with the use of KCL.
$$- \frac{V_{out2}} {R_D} = (V_{in1} - V_p) g_{m1} + \frac{V_{out2} -V_p} {r_{o1}}$$
$$\Rightarrow - V_{out2} (\frac{1} {r_{o1}} + \frac{1} {R_D}) =
V_{in1} g_{m1} - V_p (g_{m1} + \frac{1} {r_{o1}})$$
$$\Rightarrow V_p = \frac{V_{in1} g_{m1} + V_{out2} (\frac{1} {r_{o1}} + \frac{1} {R_D})} {g_{m1} + \frac{1} {r_{o1}}}$$
Secondly, we analyse the right part of this circuit with the use of KCL.
$$ \frac{V_{out1}} {R_D} = -(V_{in2} - V_p) g_{m2} + \frac{V_p -V_{out1}} {r_{o2}}$$
$$\Rightarrow V_{out1} (\frac{1} {r_{o1}} + \frac{1} {R_D}) =
- V_{in2} g_{m2} + V_p (g_{m2} + \frac{1} {r_{o2}})$$
We could substitute \$\frac{V_{in1} g_{m1} + V_{out2} (\frac{1} {r_{o1}} + \frac{1} {R_D})} {g_{m2} + \frac{1} {r_{o2}}}\$ for \$V_p\$ from what we previously got.
$$\Rightarrow V_{out1} (\frac{1} {r_{o1}} + \frac{1} {R_D}) =
- V_{in2} g_{m2} + \frac{V_{in1} g_{m1} + V_{out2} (\frac{1} {r_{o1}} + \frac{1} {R_D})} {g_{m1} + \frac{1} {r_{o1}}} (g_{m2} + \frac{1} {r_{o2}})$$
Since we already assume \$g_{m1} r_{o1} \gg 1\$ and \$g_{m2} r_{o2} \gg 1\$
$$\Rightarrow V_{out1} (\frac{1} {r_{o1}} + \frac{1} {R_D}) =
- V_{in2} g_{m2} + \frac{V_{in1} g_{m1} + V_{out2} (\frac{1} {r_{o1}} + \frac{1} {R_D})} {g_{m1}} (g_{m2})$$
$$\Rightarrow V_{out1} (\frac{1} {r_{o1}} + \frac{1} {R_D}) =
- V_{in2} g_{m2} + V_{in1} g_{m2} + V_{out2} (\frac{1} {r_{o1}} + \frac{1} {R_D}) \frac{g_{m2}} {g_{m1}}$$
$$\Rightarrow V_{out1} (\frac{1} {r_{o1}} + \frac{1} {R_D}) - V_{out2} (\frac{1} {r_{o1}} + \frac{1} {R_D}) \frac{g_{m2}} {g_{m1}}= V_{in1} g_{m2} - V_{in2} g_{m2} $$
We also assume \$r_{o1} \gg R_D\$ and \$r_{o2} \gg R_D \$
$$\Rightarrow V_{out1} (\frac{1} {R_D}) - V_{out2} (\frac{1} {R_D}) \frac{g_{m2}} {g_{m1}}= V_{in1} g_{m2} - V_{in2} g_{m2} $$
$$\Rightarrow (\frac{1} {R_D}) (V_{out1} - V_{out2} \frac{g_{m2}} {g_{m1}})
= V_{in1} g_{m2} - V_{in2} g_{m2} $$
For third equation.
$$- \frac{V_{out2}} {R_D} = \frac{V_{out1}} {R_D}$$
$$\Rightarrow - V_{out2} = V_{out1} $$
Substitute \$-V_{out2}\$ for \$V_{out1}\$
$$\Rightarrow (-\frac{1} {R_D}) V_{out2} (1 + \frac{g_{m2}} {g_{m1}})
= g_{m2} (V_{in1} - V_{in2}) $$
The gain will be
$$\frac{V_{out2} - V_{out1}} {V_{in1} - V_{in2}}
=
\frac{2 V_{out2}} {V_{in1} - V_{in2}}
=
\frac{2 g_{m2}} {-\frac{1} {R_D} (1 + \frac{g_{m2}} {g_{m1}})}
$$
$$\frac{V_{out2} - V_{out1}} {V_{in1} - V_{in2}}
=
- \frac{2 R_D g_{m2}} {(1 + \frac{g_{m2}} {g_{m1}})}
$$
As we all know \$g_{m2} = 2 g_{m1}\$
$$\frac{V_{out2} - V_{out1}} {V_{in1} - V_{in2}}
=
- \frac{2 R_D g_{m2}} {(1 + 2)}
=- \frac{4 R_D g_{m1}} {3}
$$
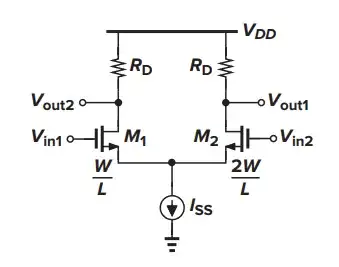

id1 = (Vin1 - Vin2)/(1/gm1 + 1/gm2) Vout = Vout1 - Vout2 = id1*RD - (-id1)*RD = 2id1*RD = 2RD(Vin1 - Vin2)/(1/gm1 + 1/gm2) So Vout/(Vin1-Vin2) = 2RD/(1/gm1 + 1/gm2) = 4/3*gm1*RD with gm2 = 2*gm1– internet Dec 16 '23 at 14:00