Input Resistance: Why can you ignore current sources?

Question

This may be a weird question, but I simply can't figure out, why you can entirely ignore current sources when calculating the input resistance of circuits.

Here is an example (it's actually a small-signal model of a BJT-circuit):

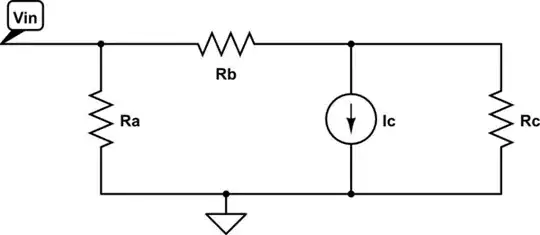
schematic

^{simulate this circuit – Schematic created using CircuitLab}

When you want to find \$R_{in} = \frac{V_{in}}{I_{in}}\$ you end up with \$R_{in}= R_a\,||\,(R_b + R_c)\$ (at least that's what the sample solution sais).

However, intuitively I was thinking: When there is a lot of collector current flowing around, with \$R = U \cdot I\$ the resistance will go up. And only when there is almost no collector current left \$(I_C \to 0)\$, I was expecting:

\$R_{in} = \dfrac{V_{in}}{I_{in}} = \dfrac{(R_a\,||\,(R_b + R_c)) \cdot I_{in}}{I_{in}} = R_a\,||\,(R_b + R_c)\$.

But obviously that is always the case. Can anyone explain to me, what I'm missing here?

From the great Wiki "The internal resistance of an ideal current source is infinite." https://en.wikipedia.org/wiki/Current_source — JIm Dearden, Jul 06 '13 at 20:11

score 4 · Accepted Answer · answered Jul 06 '13 at 20:34

Say you have this circuit, and you apply some voltage to the terminals on the left:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

What's the input impedance? \$1\Omega\$, obviously. Why? Say we want to increase the current by \$1A\$. By how much will be have to increase the current? By Ohm's law:

$$ E = 1A\cdot 1\Omega = 1V$$

That is, we need to increase the voltage by \$1V\$ per \$1A\$. That is, one ohm is one volt per ampere:

$$ 1\Omega = \frac{1V}{1A} $$

Consider this circuit:

schematic

^{simulate this circuit}

How much must voltage increase to increase current by \$1A\$? It takes a much larger increase in voltage to increase the current now:

$$ 1k\Omega = \frac{1000V}{1A} $$

What about this circuit?

schematic

^{simulate this circuit}

What about this one?

schematic

^{simulate this circuit}

By how much would you have to increase the voltage to increase the current? You can't. As the input impedance approaches infinity, the change in current per change in voltage becomes less. In the limiting case, the load is a current source that never changes, and input impedance is infinite.

Here's another thought experiment. Consider these circuits:

schematic

^{simulate this circuit}

How does the current vary in each as the load is varied? As the series resistance (R1 or R2) increases, the current varies less with load. If \$R_{load} \ll R_2\$, then the current hardly changes at all. In the limiting case, when that resistance is infinite, current doesn't change at all, and you have a current source. Of course you can't pass any current through an infinite resistance, but then you can't have an ideal current source, either.

Did you intend to increase V2 as well as R2 in your last example? While what you say is true, I would have expected you to set things up so that the current through the load was the same in both examples... (Although, yes, 1MV does seem a bit extreme) — Rupert Swarbrick, Jul 07 '13 at 20:49
@RupertSwarbrick I see your point. I was only thinking about the change in current, and not its absolute value. Although the current in V2 will be much less than V1, the current is more stable, if the load is variable over the same range in each. — Phil Frost, Jul 08 '13 at 00:45

Alfred Centauri · Answer 2 · 2013-07-06T20:45:27.343

Essentially, you're finding the Thevenin resistance looking into the input port and that resistance does not depend on the value of any independent sources. The effect of the independent sources is fully described by the Thevenin (Norton) voltage (current) source.

Consider the very simple example where we set \$R_b = 0\$ and remove \$R_c\$. We're left with a Norton equivalent circuit. Further, we see that the input current is just:

\$I_{in} = \dfrac{V_{in}}{R_a} + I_C = \dfrac{V_{in}}{R_{in}} + I_C\$

The point to take away from the above is that the input resistance is ratio of the input voltage to input current when all independent sources are zeroed.

When \$I_C = 0 \$, the current source is an open circuit (no current through for any voltage across). Thus, you might say they can be ignored, i.e., replaced with open circuits, when calculating the equivalent resistance.

Again, this only applies to independent sources. A dependent or controlled source will, in general, change the equivalent resistance and cannot be ignored.

Thank you very much! But in this case, Ic is controlled by the base-emitter voltage, which is Vin. So it's a coincidence that the voltage source can be ignored? — , Jul 06 '13 at 21:06
@shynion, one can't actually ignore it if it's a controlled source. However, you've drawn this as an independent source. Do you have a link to the actual circuit you're asking about? — Alfred Centauri, Jul 06 '13 at 21:18

Input Resistance: Why can you ignore current sources?

2 Answers2