6

My objective is to learn how to predict the output to a sqaure wave given R1, R2, R3 and Q1 datasheet (not specifically the 2N3904) without using SPICE or any other software

I was looking on google for a good source but could not find something specific enough that regards transistor parameters to that specific circuit and hoped for insight from you guys

PS: input source is 1 ohm

schematic

simulate this circuit – Schematic created using CircuitLab

Charls Diven
  • 103
  • 1
  • 6
  • Your question appears to be "Here is a circuit, what is the formulaic answer that describes the output signal completely given unknown values of Vin, Voffset, Frequency input and Vsupply" – Andy aka Oct 01 '13 at 13:09
  • Hi Andy, my objective is to learn how to pick the correct transistor and resistors for a required response time so basically you are correct. but its not like this is a "please do my work" question. i looked in many sites and some books and although i am sure the knowlege is out there it seems i need to dig too much to find the answer for that question. the books and lectures mostly explain how the transistor works and how to build circuits while the articles which refers to the transistor parameters are too basic and not specific. – Charls Diven Oct 01 '13 at 13:47
  • Well, for a given input waveform, you could use a simulator to help you understand general trends and as for the transistor, whether you need high speed or low speed always choose one that suits your fastest needs, You'll probably need to include an emitter resistor to linearize things too. – Andy aka Oct 01 '13 at 14:13
  • Let me see if I understood your question: given that the input is a square wave voltage having a predefined frequency (yes, the frequency is also a factor!), you want to be able to draw the collector's voltage waveform, and be able to predict how the values of resistors and transistor's parameters will affect the output. Is the above a correct description of your task? – Vasiliy Oct 01 '13 at 20:12
  • 2
    Possibly useful search term : "Miller capacitance" –  Oct 01 '13 at 20:35
  • Yes Vasily that is correct. The reason is that i need to know how certain protocols will look to a microcontroller. if for example a certain protocol is using '1' as 50us high and '0' is 80us high i would like to make sure the pulses won't be clipped by the transistor – Charls Diven Oct 02 '13 at 05:31
  • The result will depend very much on whether the transistor will be saturated or not. So you have to consider different cases depending on all of your parameters (Vin, Vcc, R1, R2, R3, β) – Curd Oct 02 '13 at 09:01
  • Thanks Curd, i believe Ran.CohenTawil answered my question. Best Regards – Charls Diven Oct 03 '13 at 13:41

1 Answers1

0

Most of the information can be found in "The Art of Electronics" by Horowitz and Hill

In order to understand transistor response time it is required to understand the next:

  1. Storage time (ts): the time the transistor requires in order to come out of saturation. i.e. when the transistor is saturated it contains a certain deposit of charge that takes time to be depleted. If you place an oscilloscope comparing a step drop at the input with your output you will notice a time the output does not even start to rise, that is mainly the time the transistor is depleting its charge (ts)

  2. Ccb: capacitance between collector and base. Although there are other parasitic capacitance at the transistor this is the most influential one. you should find this value in all the transistors datasheets. The smaller the value the better the response time of the transistor.

Ignoring the ts for a second lets assume R3, Ccb and Cl (load capacitance you did not include in your schematic) is relatively big. the collector rise will look exponential due to these component combination and the rise time (10-90%) will be approximately:

2.2*R3*(Cl + Ccb)

If on the other hand these values are quite small that still doesn’t mean the rise will be a step. In that case the phenomenon that will dominate the rise will be that the current through Ccb will act as a negative feedback to the base that will limit the rise and instead of an exponential rise you will get a ramp

In essence, many square wave response will start as a ramp and end up as exponential. The way to make a prediction about the rise time is first to determine the point where the rise is turning from a ramp to exponential via the next formula:

VX = Vcc - Rc * ((Vbe - Vin(low) / Rs ) + Cl*(dVc/dt))

while:

dVc/dt = (Vbe - Vin(low))/(Ccb*Rs)

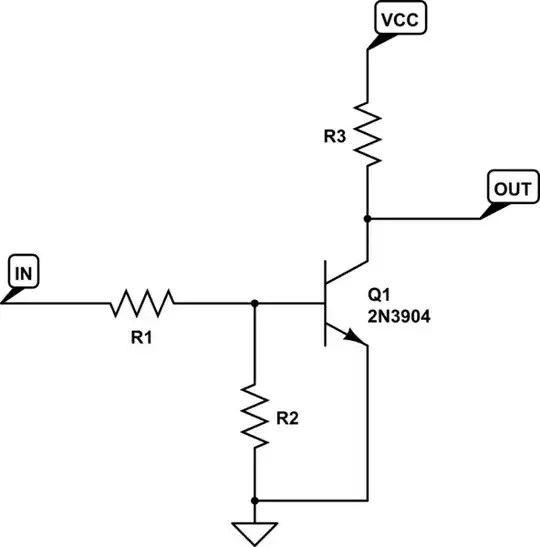
In your circuit:

Rs = R1 || R2

Vbe = 0.7V (basically)

Vin = if other than 0V use Thevenin to calculate

If that value is negative the rise is entirely exponential and the rise time (10-90%) can be derived from:

2.2*R3*(Cl + Ccb)

Else calculate the time the ramp (dVc/dt) will reach Vx and add to it the time from Vx to the 90% reach using the exponential formula

as for the fall time you can use the next formulas:

-dVc/dt = ( 1 / (Cl + (Hfe + 1)*Ccb) * ( Hfe * ((Vin(high) - Vbe)/ Rs) - (Vcc - Vc)/Rc)

Tf = 0.8*Vcc / (dVc/dt)

Note that at the first formula Vc can be sometimes negligible and can be discarded, otherwise, you will need to calculate it in several steps to get a good estimate

Other notes:

Hfe is relative to your signal frequency and you should derive the correct value from the datasheet

Storage time: although this is a value that is related to the transistor, there are methods to lower its effect. Look for "Baker clamp" and "speedup capacitor" on that.

These are crude estimates and should be backed up (datasheet graphs, SPICE and actual testing's)

Ran.CohenTawil
  • 117
  • 4