An exact theoretical analysis of this is rather involved so I will take an approximate approach.
We can idealise the beam as a single degree of freedom (SDOF) dynamic system. The theory behind this can be found in a variety of dynamics textbooks. For example: Biggs - Introduction to Structural Dynamics (1964).
Because the beam has uniform mass and stiffness we can obtain a Load-mass factor $K_{LM} = 0.49$ for a point load in the center of a simply supported beam. This converts the mass and load of a distributed beam into an equivalent SDOF spring-mass system by assuming a mode shape.
For the central point load it is straightforward to show that the stiffness $k = \frac{48EI}{L^3}$.
We can then calculate the circular natural frequency of the equivalent SDOF system:
$$\omega_n = \sqrt{\frac{k}{K_{LM}M}}$$
where $M$ is the total mass of the beam.
And the damped natural frequency:
$$\omega_d = \omega_n\sqrt{1-\zeta^2}$$
where, $\zeta$ is the damping ratio (in this case we take this as 0.05 since you specify 5% damping).
Taking the situation you describe, we can consider the system as having an initial velocity, which we will determine by conservation of momentum.
Velocity of the man when he impacts the beam:
$$v_f = \sqrt{2 a d} = \sqrt{2(32.2 \frac{ft}{s^2})(\frac{2}{12}ft)}=3.3\frac{ft}{s}$$
If he 'sticks' to the beam the initial velocity of the beam-man system is found by conservation of momentum:
$$ v_i (0.49 M+m)= v_f m \rightarrow v_i = v_f \frac{m}{m+0.49 M}$$
The displacement of a damped single degree of freedom system subject to an initial velocity is (see a dynamics text for derivation):
$$x(t)=\frac{v_i e^{-\zeta \omega_n t}}{\omega_d} \sin{\left(\omega_d t\right)}$$
so with
$$v_i = 3.3 \frac{ft}{s}\frac{180lb}{180lb+0.49 (120\frac{lb}{ft})(20ft)}=1.59 \frac{in}{s}$$
$$k = 48 \frac{EI}{L^3} = \frac{48(29000 ksi)(1070in^4)}{\left[(20ft)(12\frac{in}{ft})\right]^3}=108 \frac{kips}{in}$$
$$\omega_n = \sqrt{\frac{k}{K_{LM}M+m}}=\sqrt{\frac{108\frac{kips}{in}(386\frac{in}{s^2})}{0.49 (2400lb)+180lb}} = 175 \frac{1}{s}$$
$$\omega_d = \omega_n\sqrt{1-\zeta^2} = 175\sqrt{1-0.05^2}=174.8\frac{1}{s}$$
and we can now calculate the beam mid-span displacement x(t):
$$ x(t)=\frac{v_i e^{-\zeta \omega_n t}}{\omega_d} \sin{\left(\omega_d t\right)} = \frac{1.59 \frac{in}{s} e^{-0.05 (175\frac{1}{s}) t}}{174.8\frac{1}{s}} \sin{\left(174.8\frac{1}{s} t\right)}$$
The response is:
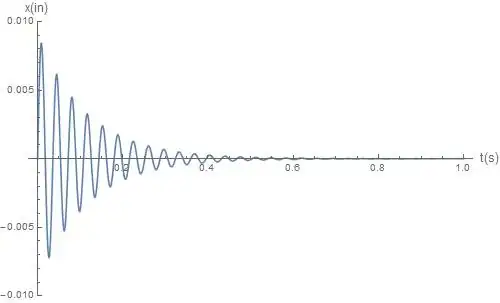
The frequency of the loading, for example due to walking, will have a large effect on the response. Especially if the frequency of loading is close to the natural frequency of the element (resonance).
For floor vibrations you may find the steelconstruction.info page on this topic interesting.
