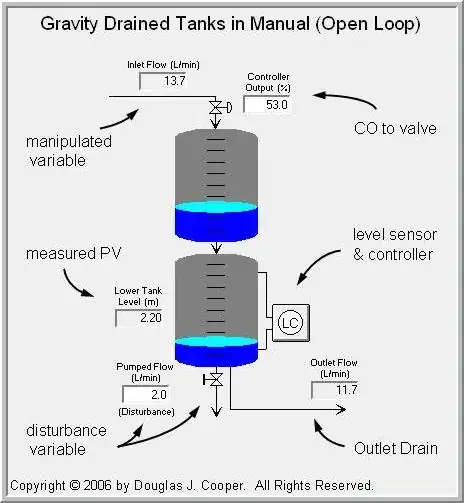
I have a system like this:
and I have to estimate the height of the lower tank.
First of all, I'm considering that I have a non-viscous, incompressible fluid in steady flow.
Base apertures
The outlet velocity of liquid when draining a tank or a container can be expressed as: \begin{equation} v = C_v \sqrt{2gH} \label{eq:baseAperture1} \end{equation} where $v$ is the outlet velocity $[m/s]$, $C_v$ is the velocity coefficient (water: 0.97), $g$ is the acceleration of gravity ($g=9.81 m/s^2$) and $H$ is the height $[m]$.\ The volume flow can be expressed as: \begin{equation} V = C_d A \sqrt{2gH} \label{eq:baseAperture2} \end{equation} where $V$ is the volume flow $[m^3/s]$, $C_d$ is the discharge coefficient ($C_d = C_c C_v$ where $C_c$ is the contraction coefficient (sharp edge aperture: 0.62, well rounded aperture: 0.97)) and $A$ is the area aperture $[m^2]$\\ I know the volume flow and the height, so, using the first equation I get the outlet velocity $v$. Using the second equation I can get the area A of the outlet hole (I have two possible results because I don't know if the hole has a sharp edge aperture or a well rounded aperture).
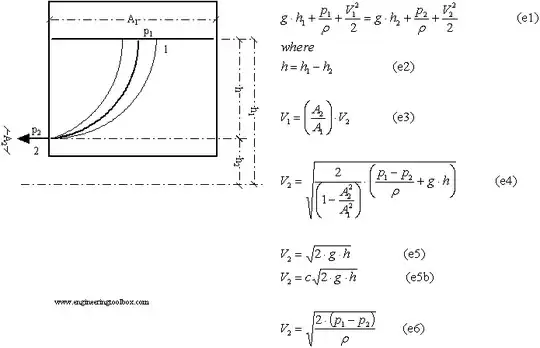
Bernoulli
\begin{equation} \frac{d}{ds} \left(\frac{v^2}{2} + \frac{p}{\rho} + g h\right) = 0 \end{equation} where $v$ is the flow speed, $p$ is the pressure, $\rho$ is the density, $g$ is the gravity and $h$ is the height.\ From the previuos equation, I get: \begin{equation} \frac{v^2}{2g} + \frac{p}{\gamma} + h = constant \end{equation} where $\gamma = \rho g$\ For a tank with a small orifice in a lateral, close to the bottom, I have:
Bernoulli part 2
Making a lot of maths, I get these two equations: \begin{equation} \dot{h}_1 = -\frac{A_{d1} \sqrt{2g}}{A_{D1}} \sqrt{h_1} + \frac{K_P}{A_{D1}}V_P \end{equation} \begin{equation} \dot{h}_2 = \frac{A_{d1}\sqrt{2g}}{A_{D2}} \sqrt{h_1} - \frac{A_{d2} \sqrt{2g}}{A_{D2}} \sqrt{h_2} \end{equation} where $h_1$ is the height of the upper tank, $h_2$ is the height of the lower tank, $A_{d1}$ is the area of the orifice of tank 1 and $A_{d2}$ is the area of the orifice of tank 2, $g$ is the gravity, $A_{D1}$ is the area of the upper tank and $A_{D2}$ is the area of the lower tank, and $V_P$ is the voltage of a pump. In my exercise, $Q_P = V_P K_P$ where $Q$ is the discharge. Is $Q_P$ the volume flow?
I know how to linearize that equations, using the Jacobian, and solving that equations but I don't have the areas $A_{D1}$ and $A_{D2}$.
How can I get $A_{D1}$ and $A_{D2}$?