2

I am trying to derive the isentropic flow equations for a compressible gas by myself and at the end, I have different formulation than the one in the literature. Can you please tell me what am I doing wrong?

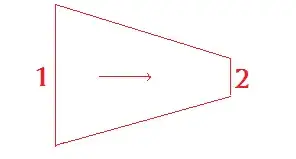
So we have a nozzle:

enter image description here

If we do an energy balance and consider that the kinetic energy and the potential energy in point 1 is negligible, one ends up with this relation: $h_1=h_2+\dfrac{v_2^2}{2}$

By using the ideal gas relation $h = CpT$, and if we then divide the equation by Cp and then by $T_2$, we end up with something like this:

$\dfrac{T_1}{T_2}=1 + \dfrac{v_2^2}{2T_2Cp}$

And finally using $Cp = Cv + R$, denoting $Cp/Cv = k$, using the formula for the mach number $M = v/c$ and the speed of sound in gas $c = \sqrt{(T_2Rk)}$, we end up with this relation:

$\dfrac{T_1}{T_2}=1 + \dfrac{k-1}{2}M^2$

But from the literature one can find that this formula is written like this:

$\dfrac{T_t}{T}=1 + \dfrac{k-1}{2}M^2$

The question is... Is the total temperature $T_t$ in their equation the same as $T_1$ in our case? And if the nozzle discharges to the ambient, is $T$ in their formulation the same as $T_2$ in ours? I'm a bit confused with the symbols and the meanings and I want to learn how this works.

P.S. This is a copy of a question from enter link description here. I have been suggested to try and ask here.

Community
  • 1
Physther
  • 614
  • 1
  • 7
  • 16

1 Answers1

0

Is the total temperature $T_t$ in their equation the same as $T_1$ in our case?

$T_t$ is called the stagnation temperature, which is the temperature of a flow when it's brought to rest ($v=0$), the $T_1$ you defined in the first equation is called the stagnation temperature since you ignored kinetic energy.

$$C_pT_t = C_pT + \frac{v^2}{2}$$ $$T_t = T + \frac{v^2}{2C_p}$$

And if the nozzle discharges to the ambient, is $T$ in their formulation the same as $T_2$ in ours?

Yes, the arbitary $T$ in the equation is for any location in the nozzle including the discharge.

Algo
  • 2,140
  • 1
  • 20
  • 34