Total lateral pressure from clay soil when hydrostatic pressure is also present

Question

I'm stuck with how to work out the total pressure and centre of pressure in this example.

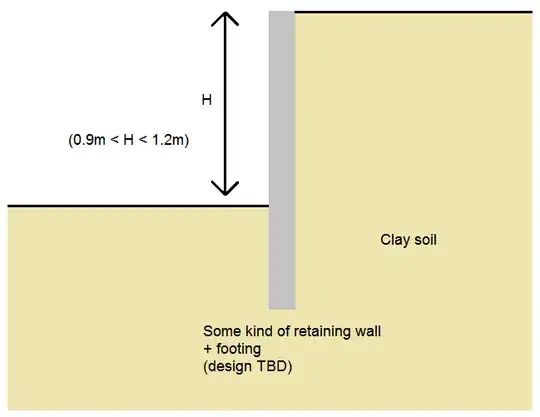
At an outdoor boundary between two properties there is a stepped change in ground level of the clay soil. The ground abruptly changes level by H (roughly 0.9 - 1.2m if it matters). A vertical retaining wall is present, whose design is not relevant here. The soil's depth is much greater than the wall height so there are no relevant local boundaries or property changes in the soil below the retaining wall (however deeply it is embedded in the soil). There are no buildings or other sources of pressure on the soil other than its own weight and soil mechanics, and hydrostatic effects of any water it contains. There is considerable rainfall at times, so the soil will periodically become saturated.

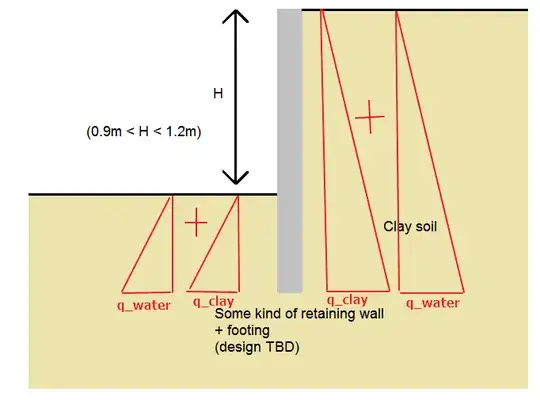
I'm ignoring for now, any other issues, such as bearing, shear and other failure modes, but for safety I should probably assume active rather than passive pressure, I think. I want to find the maximum design lateral pressure such a wall must resist in the presence or absence of built-up hydrostatic pressure, and the height above the lower ground level at which that pressure should be taken as being exerted for calculation purposes.

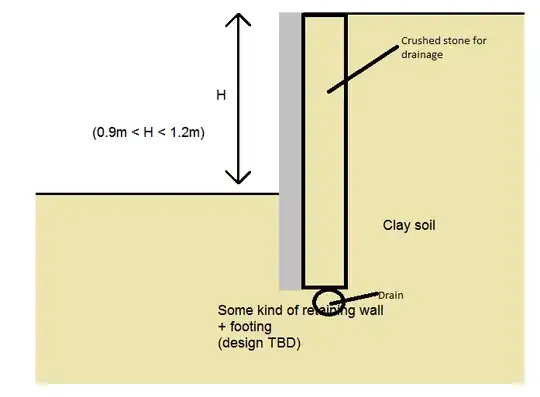
Specifically I think what I'm trying to find is the maximum design lateral pressure exerted by the soil and any ground-water on the wall, and the point at which that pressure is exerted for calculation purposes (a) if there are ample weepholes/drainage, (b) if there are no weepholes/drainage. I'm expecting the answer to depend on the characteristics of the specific clay to an extent, but I can't work out which characteristics are critical and how much they affect the answer.

Update Sketch as requested:

Answer 1

Usually since hydrostatic pressure along with freezing and thawing are such a pain (quite hard to figure out the pressure from freezing water in soil), in practice I try and keep my retaining walls 100% water free.

However, if you were to design the wall for lateral earth pressure of clay + water table pressure, I found in my old notes some active, rest and passive values for clay which are around :

$k_a = 0.6 \\ k_o = 0.7 \\ k_p = 1.7$

Usually you will start with a hypothesis (which side is active or passive or at rest), and then confirm that your had chose correctly with maximum displacements. Since your aren't analysing the wall yet, we will keep that for later.

For safety, you should probably at least consider at rest pressure on both side (use $k_o$ for both sides) and verify your wall displacements afterwards (If you consider active pressure on the right hand side, this means your wall is relatively flexible and the soil can mobilise some of its shear stiffness).

Usually for safety, we also put the water table all the way up to the level of the ground, since this can easily happen after a storm in non-draining clay. You then apply your basic soil equations, first dry-soil pressure and add water pressure (both triangular loads). In this case we assume there is no external load on top of the right hand side of the wall.

The equations for the maximal pressure are the same for each side:

$ q_{clay} = k * \gamma_{clay} * H \\ q_{water} = k * \gamma_{water} * H $

If ever you decide to design this wall, you will see that your critical moment and shear will be at the base, even if you have some soil supporting on the left hand side. If you have enough movement to mobilise active pressure on the right and passive pressure on the left, then you can simply use the same equations with $k_a$ on the right and $k_p$ on the left.