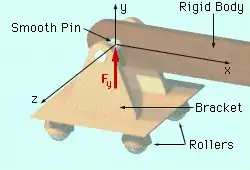
When talking about roller supports in a statics problem, we say that the roller prevents only the vertical translation of the beam, but not the rotation or the horizontal translation of it. So there is only one vertical reaction applied on the beam by the roller.
Also, we know a beam is connected to the roller using a pin, and the reaction force is the result of the pin that acts on the beam, as shown in this picture:
Now, suppose that I have a beam that is connected to a roller and I am going to push the beam in the horizontal direction (rollers don't prevent translation in the horizontal direction). What reactions should I expect?
I think that the pin is going to apply a force in the horizontal direction (due to the contact between the pin and the beam), which means that there is a reaction force in the horizontal direction. Is that true? If it is true, then why don't we consider horizontal reactions when analyzing rollers?