Undamped forced vibration for a multi dof system

Question

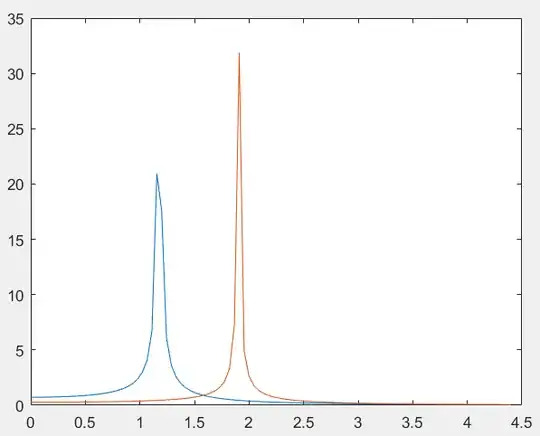
I'm trying to determine the amplitude vs the excitation frequency of a multi dof dynamic system. I'm very confused from reading different methods, although I understand there's a very general one, which is not giving me the results that I think should be when plotting the response. Considering a system with no damping $\mathbf{M{\ddot x}+{Kx}=F(t)}$, and by assuming the harmonic excitation of the force is a cosine the system becomes $\mathbf{-MX{cos(\omega t)}+{KX}cos(\omega t)=fcos(\omega t)}$. From here the cosines get cancelled out so only $\mathbf{[K-M{\omega^2}]X=f}$ remains. By solving for the $X$ vector in the end I get $X = \frac{F/M}{|\omega_n^2-\omega^2|}$.

So with Matlab I wrote the following code, with parameters I found on an example from brown.edu, in which the explanation is not complete, my system is actually a 24 DoF system, so I need the code a bit automated:

    k1 = 2;
k2 = 1;
k3 = 1;
m1 = 1;
m2 = 1;

M=[m1 0; ...
   0 m2];
K=[k1+k2 -k2; ...
  -k2 k3+k3];
F=[1;...
   1]; 

[V,D] = eig(K,M);      
D     = diag(sqrtm(D)); 
frequencies   = (D);           
[rows,~] = size(V);

f=linspace(0,0.7,100);
omega=2*pi*f;
Mag = M\F; 
Xt = zeros(rows, length(omega));
    for i = 1:rows
        for j = 1:length(omega)          
            Xt(i,j) =  abs((frequencies(i)^2 - omega(j)^2)\Mag(i)) ;
        end
    end
figure
    for m = 1:length(frequencies)
        plot(omega, Xt(m,:));
        set(gca,'YScale','log')
        hold on
        axis tight
    end

Where the main part is the Xt(i,j) = (abs (frequencies(i)^2 - omega(j)^2)\Mag(i) ); , which follows the determined formula for the displacements of each degree of freedom.

When plotting what I get is:

which shows the masses vibrations being at resonance, but from what I understand there should be more peaks and some antiresonance.

What am I missing in the general math?

EDIT_1: I changed the bit of the code to calculate the absolute values of the equation like: $$X(\omega) = \left|\sum_n \frac{F/M}{\omega_n^2 - \omega^2}\right|$$ but I get the same when plotting. I found another solution but I don't understand how its determined or why choose it. From ${M{\ddot x_i}+{Kx_i}=f(t)sin\omega t}$ the steady state solution is $x_{iss} = x_{is} sin \omega t + x_{ic} cos \omega t$ , where $i = 1,2$ , then $$ \begin{bmatrix} \mathbf{-(\omega)^2M+{K}} & \mathbf{0} \\ \mathbf{0} & \mathbf{-(\omega)^2M+{K}} \end{bmatrix} \begin{bmatrix} \mathbf{x_{ic}} \\ \mathbf{x_{is}} \end{bmatrix} = \begin{bmatrix} \mathbf{0} \\ \mathbf{f} \end{bmatrix} $$ which is then solved to get ${X_{i}} = (x_{ic} + x_{is} )^{1/2}$ First, I don´t understand very well if just $x_{iss}$ is substituted in ${M{\ddot x_i}+{Kx_i}=f(t)sin\omega t}$ for $x_i$. And is this just assuming a sum of $cos$ and $sin$ instead of my first approach of only $cos$? Then, do I need to consider adding the transient response also, which I´m actually not sure how it would be.

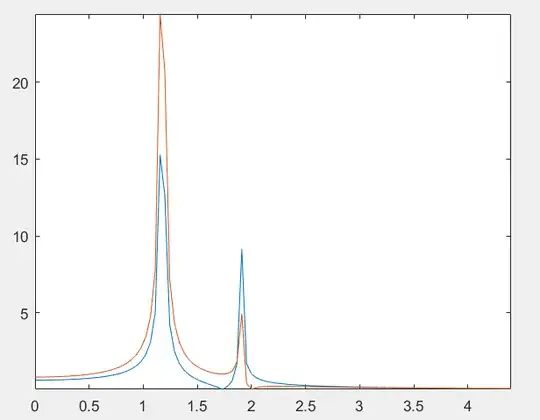
EDIT_2: I think I figured out what I was doing wrong. I changed the equation from $$X(\omega) = \left|\sum_n \frac{F/M}{\omega_n^2 - \omega^2}\right|$$ to $$ X = [K-M\omega^2]^{-1}F$$ which mathematically I though they were the same??? The code part that changed is as follows:

for j = 1:length(omega)       
       Xt(:,j)  =  abs((K-M*omega(j)^2)\F);
    end
figure
    for m = 1:length(frequencies)
        plot(omega,Xt(m,:))
        hold on
        axis tight
    end

And the result plot is:

For my extended MDoF system I got:

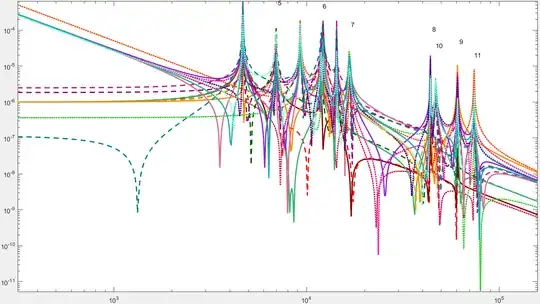
In which I excited all DoF, even when I only excite a single one, it is still very hard to notice what's going on, is there a better way of analysing the response?

alephzero · Accepted Answer · 2017-08-11T01:32:32.477

The code in your OP seems to be for a 2 DOF system not a 24 DOF system. You could check that by printing the "frequencies" variable from your eigensolution.

The reason you are not getting anti-resonances is because you are taking the absolute values in the wrong place. You should be calculating $$X(\omega) = \left|\sum_n \frac{F/M}{\omega_n^2 - \omega^2}\right|$$ not $$X(\omega) = \sum_n \frac{F/M}{\left|\omega_n^2 - \omega^2\right|}$$

The contribution to $X$ from each mode changes its phase by 180 degrees, and therefore changes sign, when the frequency passes through the corresponding $\omega_n$. The antiresonances occur when the contributions from different modes cancel out.

Note, you will probably see the antiresonances better on a plot if you use a log scale for $X$.

EDIT following comments by the OP:

You also need to decompose $F$ into its modal components and apply them to the corresponding terms in the sum. If $$M\ddot x + K x = F.$$ Pre-multiply by the eigenvectors $\Phi$: $$\Phi^T M\ddot x + \Phi^TK x = \Phi^T F$$ But you know $\ddot x = -\omega^2 x$, so $$(-\omega^2 \Phi^T M + \Phi^TK) x = \Phi^T F$$ Also $\Phi^T M \Phi = I$ for mass-normalized eigenvectors, and $\Phi^T K \Phi = \text{diag}\,(\omega_n^2)$, so inserting $\Phi \Phi^{-1}$ into the left hand side gives $$(-\omega^2 + \text{diag}\,(\omega_n^2)) \Phi^{-1}X = \Phi^T F.$$ Decomposing $X$ into its modal components gives $$X = \sum_n \Phi_n\xi_n,$$ so you end up with the decoupled equations $$(-\omega^2 + \omega_n^2) \xi_n = \Phi_n^T F$$.

In other words, if $\mathbf{f}$ is the vector applied forces, the $F$ in each term of your sum should be $\Phi_n^T \mathbf{f}$ where $\Phi_n$ is the $n$th column of the eigenvector matrix.

Finally, you need to recombine the $\xi_n$ to get $X$, and then take its absolute value.

Undamped forced vibration for a multi dof system

1 Answers1