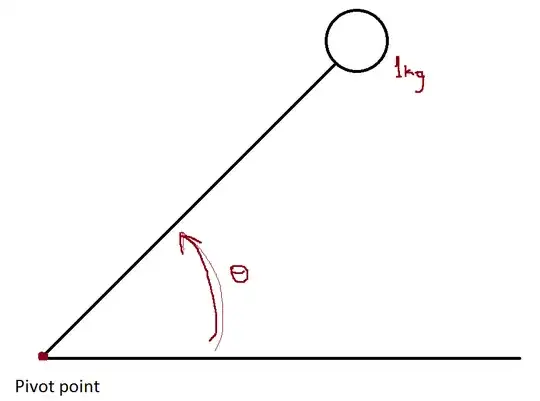
The equation should be
$$ J \, \ddot{\theta} + K \, (\theta-\theta_T) + C \, \dot{\theta} =0 $$
where $\theta_T$ is the target angle and the rest position for the spring.
Things simplify wit the following substitution
$$ \begin{cases}
K = J \Omega^2 \\
C = 2 \zeta J \Omega
\end{cases} $$
where $\Omega$ is a parameter the relates to the stiffness, and $\zeta$ a parameter that relates to the damping.
The general solution of the equation $\ddot{\theta} + \Omega^2 (\theta-\theta_T) + 2 \zeta \Omega \dot{\theta} =0$ is
$$ \theta = \theta_T + C_1 \exp\left( -\Omega t \left(\sqrt{(\zeta^2-1)}+\zeta \right) \right)+ C_2 \exp\left( -\Omega t \left(\sqrt{(\zeta^2-1)}-\zeta \right) \right) $$
where the coefficients $C_1$ and $C_2$ are found based on the boundary conditions. In this case, the rod is at rest when $t=0$ and thus
$$\begin{cases}
C_1 =\frac{ \theta_T}{2} \left( \frac{\zeta}{\sqrt{(\zeta^2-1)}}-1 \right) \\
C_2 =-\frac{ \theta_T}{2} \left( \frac{\zeta}{\sqrt{(\zeta^2-1)}}+1 \right)
\end{cases} $$
The fastest response is when $\zeta \rightarrow 1$ since that minimizes the value of the first exponent. With optimum damping the solution becomes
$$ \theta = \theta_T \left( 1 - {\rm e}^{-\Omega t}(1+\Omega t) \right) $$
and $C = 2 J \Omega$.
But as you stated, you cannot find the correct $\Omega$ to reach the target angle at the specified time because $\Omega$ cannot be isolated from the solution.
But it can be isolated from the general solution when $\zeta>1$. From the two terms, the first one approaches zero much faster than the second one. We can find the coefficient $\varphi = \Omega t$ which makes the second exponent near zero by a value $\epsilon$ (in degrees).
$$ \left. \frac{ \theta_T}{2} \left( \frac{\zeta}{\sqrt{(\zeta^2-1)}}+1 \right) \exp\left( -\varphi \left(\sqrt{(\zeta^2-1)}-\zeta \right) \right) = \epsilon \right\} $$ $$ \varphi = \frac{ \ln\left( 2 \frac{\epsilon}{\theta_T} ( \zeta \sqrt{(\zeta^2-1)}-\zeta^2+1)\right)}{\sqrt{(\zeta^2-1)}-\zeta} = \Omega\, t_T $$
where $t_T$ is the target time. A good compromize occurs when $\varphi = \frac{1}{\sqrt{(\zeta^2-1)}}$ which makes $\frac{{\rm d}\varphi}{{\rm d}\zeta}=0$ and hence minimizes $\varphi = \Omega \, t_T$.
This produces the solution
$$\begin{cases}
K = \frac{J}{t_T^2 \gamma (\gamma+2)} \\
\zeta = \frac{ \sqrt{(J+K t_T^2)}}{t\,\sqrt{K} } \\
C = \frac{2}{t_T} \sqrt{J (J+K t_T^2)}
\end{cases} $$
where $\gamma \ll 1$ is a small positive value (defined as $\zeta = 1+\gamma$).