I kind of have an intuition or at least imagination about how fillet|chamfer of inner edges|vertexes reduce stress (concentration).
But does that apply to outer edges|vertexes aswell? Maybe to a lesser degree or not at all?
So should one use outer fillets|chamfers for this reason?
(Lets take a thin hollow brick-shaped object (case or box) as an example.)
Sorry for not taking your "Thin Hollow Brick-Shaped Object" as an example - I felt a standard notched test specimen would illustrate the principle more clearly:
It can be seen that adding external radii to the test sample has no effect on the stress. In this example, cutting even more material away from the corners would make no difference to the failure of the sample, since that would always occur at the point of highest stress, i.e. the root of the notch.
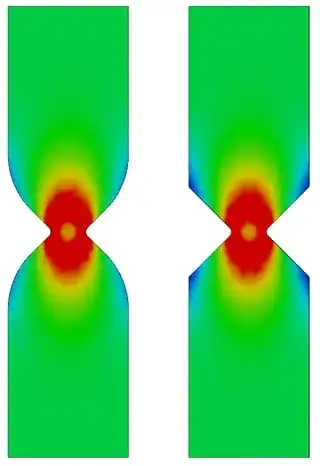
Edited to add: in a 90-degree bend specimen, the removal of material on the external edge will actually cause an increased stress on any corresponding internal edges, since there is a reduced cross sectional area over which the stress can be spread.
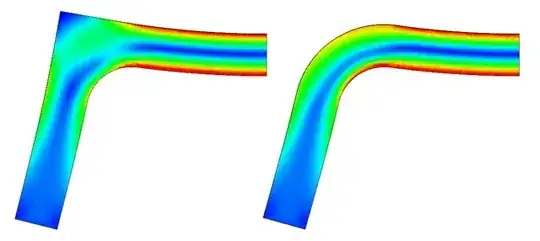
That said, there are real-world examples where ommitting an external radius might cause a component to fail early, but these do not fall within the theoretical scope of your question. For example, it is desirable in injection moulded components to keep the wall sections as constant as possible so that the plastic can cool evenly. If your 'hollow brick' example had internal radii, but none externally, then the plastic would be locally thicker, cool more slowly, and this could introduce voids or residual stresses that would not otherwise have been present.
