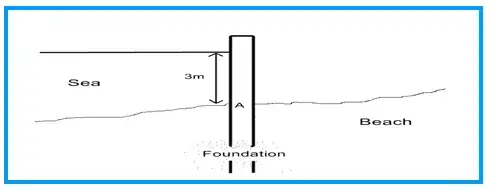
Usually with this kind of problems what I would do is to analyse what effect is caused by what source. In your specific problem, there is water under gravitational load. The gravitational field imposes a vertical pressure distribution inside the water. This pressure acts on the wall.
Thus the first answer I would give is the distribution of pressure $p$ as a function of the gravity of earth $g$, the density of water $\rho$ and the vertical coordinate $z$ (I would choose $z=0$ at sea level and positive values of $z$ going downward, but you can choose a different coordinate system). This gives you a function $p(z)$. This is not directly asked for, but is required to answer the two questions.
In the second step, since the load is distributed, I would integrate this distributed load (force per unit length) along the height:
$$
F=\int_0^h w \cdot p(z) \, \mathrm{d}z
$$
with width $w=6\,\mathrm{m}$ and height $h=3\,\mathrm{m}$. The distributed load is the product of pressure and wall width, because the pressure does not vary with width. If it did, I would have to integrate not only along the height axis $z$, but also along the width axis.
Finally, to calculate the momentum, I would integrate the local torque, with is the product of the distributed load $w \cdot p(z)$ and the lever arm length $(h-z)$:
$$
M=\int_0^h w \cdot p(z) \cdot (h-z) \, \mathrm{d}z
\quad\mbox{.}
$$
Now you can calculate everything and check if my results are the same as yours. :-)