How can I determine the required thickness of these plate materials?

Question

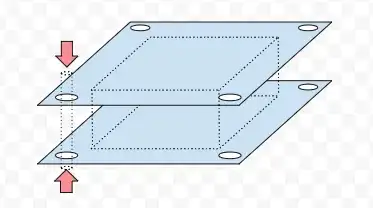
I am designing something with a sandwich construction that needs to squeeze the internal layer uniformly. The lower plate is to be made from cast iron and the upper plate needs to be made from copper. The squeezing will be done with four threaded rods, nuts and some spring washers.

The squeezing force I need to apply is 30720N, so I guess 7680N per nut (or is it not so simple?). And what I really don't know is, how do I determine a thickness of material required, given its properties and my design details? My requirements are

1. Plates will not deform like playdough between 20˚-150˚C
2. Plates will not buckle like a spring very much, so that the sandwich pressure is not applied unevenly.

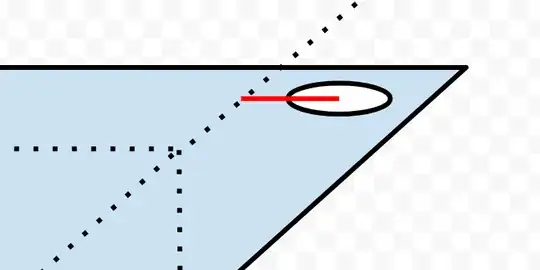
kamran's answer describes the red line below as the lever distance in his model.

I have tried my best to read up on Young's Modulus and Shear Modulus, etc., but I do not grok how to correctly apply these to real life.

Question: Can someone kindly point me to a formula or a workflow so that I can calculate the answer myself?

Answer 1

First off you want to make sure if you should divide the required squeezing force by four. Assuming that is correct we can proceed.

Because of symmetry you can assume the flange overhang will have to resist a bending moment that would want to bend it down like a cantilever slab.

There are actually many steel column base-plates that are loaded very similar to this and by checking a column base-plate design manual you'll find an identical configuration and use the equations and recommendation there.

An alternative as a reasonable simplification is to assume the plate's bending moments, once on x-x direction and then on y-y direction, so we disregard the stress concentration at the corner and assume the flange is under a concentrated load by one bolt acting at the distance measured perpendicular to the edge of the plate from center of the bolt to inside edge (0.707 x your call out distance), let's call it $l$, and let's call your bolt tension $p$.

So your moment is $ M= pl$

your slab bending moment $I=bh^3/12$

Where $b$ is your plate width and $h$ is its thickness.

Now your stress $\sigma =My/I= Mh/2I$

And you can test if your plate is strong enough to support the bolt load if you have its allowable stress. The only catch is you apply only one bolt tension per edge.

Answer 2

From the information you've given it is difficult to be too specific, but looking at the loads and design you might get some ideas by considering elastomeric bridge bearing plates or sole plate design standards.

A couple of useful references may be found for bearing plates and sole plates.

There is also another post that considers stiffness versus thickness of steel plate here. Essentially it comes down to stiffness, which is a function of Moment of Inertia and Modulus of Elasticity.

Answer 3

Okay, you're not going to like this answer, but you need to space the individual devices in the array to accommodate intermediate fasteners. The assembly as you drew it would cost a couple hundred dollars in materials and fabrication, and would be very heavy. So leave 3 6mm gutters between devices perpendicular to the wire gutters, drill a 6mm hole between each unit, drop in a 4x4mm nylon shoulder washer, and install a 4M machine screw. This gives you 12 intermediate fasteners. Then run 16 more around the perimeter. These last could be 3M in a 3x4mm shoulder washer if you wanted to get fussy. This gets the thickness of copper down to about 6mm for good results. Going with fancier spring isolation washers of at least 10mm dia can get you down to 5mm copper. A happier solution would be to find a Peltier form factor that has fastener notches so you can close-pack them.

The fact that you have a thermal gradient across the copper makes it want to distort. So you don't really want too thick of a copper plate, the thermal distortion forces would soon overwhelm the clamping forces.