Convolution with RTD laminar flow

Question

I have laminar flow in a tube. Consider the tube to be 0.2 m long and with an average velocity of 0.05 m/s. The analytical expression for my transfer function is: $E(t)= \frac{\tau^2}{2*t^3}$ for $t$>=$\frac{\tau }{2}$ and $E(t)=0$ for $t < \frac {\tau }{2}$. $\tau$ is the mean residence time. In this case: $\tau$=0.2m/0.05m/s=4 s. I want to convolute this with an exponential equation: $E_2=(1-exp(\frac{-t}{2.55}))$. This equation descripes the magnetization of a particle in a static magnetic field.

I want to get the average magnetization of the particles at the outlet of the tube. So I thought I would do the following: $E_{out}(t)=E(t)*E2(t)$. I would then take the value at t=4s. I have the results from CFD which gives the following: CFD result, the red line is the magnetic field and the green line is $E_{out}(t)$. I'm interested in the value at x=0,2m which is 0.7942.

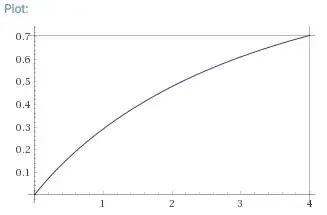
My results of the convolution are totally different:Convolution result

What am I doing wrong? I'm a little bit confused. Has anyone an idea of how to approach this problem.

Best regards,

Gesetzt

Answer 1

The average magnetization exiting the tube in steady state should just be the product not the convolution. $$\int_0^\infty E(t)\, E2(t) \, dt$$ $$\int_{\frac{\tau}2}^\infty \left(1-e^{-t\frac{t}{k}}\right)\, \frac{\tau^2}{2\,t^3} \, dt$$ $$-\frac{\tau^2 Ei\left(-\frac{\tau}{2 k}\right)}{4 k^2} - \frac{\tau \, e^{-\frac{\tau}{2 k}}}{2 k} + e^{-\frac{\tau}{2 k}}-1$$ Where $Ei$ is the Exponential Integral

This looks like it comes out to a bit less than your CFD results:

The x axis in this case is the average residence time which should be proportional to the length along the tube, making our plots comparable.