Calculate force to lift piston from a given closing pressure

Question

I am trying to calculate the force required to close the valve on an annular blow-out preventer. A rubber ring (called a packing unit) closes around the pipe when a force is applied from underneath, as shown here:

The actual valve has the hydraulic fluid coming into a chamber that goes the around the outside of the main body, which then lifts a piston which applies the force to the packing unit, as shown here:

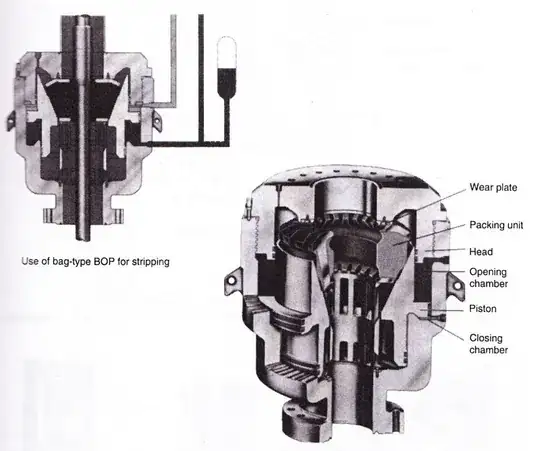
_{(source: geologie.vsb.cz)}

In the documentation for the bop it says that the hydraulic pressure required to close or open the valve is 3000 PSI.

From this, how do I calculate the force to close the valve?

I assume you just multiply 3000 by the area the pressure is acting on:

$$3000*6894.7*(\pi R_o^2 - \pi R_i^2)$$

Where $R_i$ and $R_o$ are the inner and outer radius of the ring, shown in the picture in the second link. Units of these are meters. $6894.7$ is to convert from PSI to N/m².

But this gives a HUGE force. Am I doing something wrong in the maths? Or am I interpreting the documentation wrong. Does a 3000 PSI closing pressure not mean that you have to apply 3000 PSI of pressure to the hydraulic fluid acting on the outer ring of the piston? Maybe it means that 3000 PSI is needed to squish the packing unit so it closes? In this case what information do I need and how do I calculate the force required to close the valve?

Answer 1

Roark's Table 15.3, Case 1e has a formula on the rubber ring, just to check your math if you want to.

For the inside radius to compress to 0, we'd need a compression force to equal:

$$ \frac{\text{Total Closing Force}}{\text{Volume of Rubber Ring}} = \frac{3E}{R_o(\frac{R_i(1-\nu)}{R_o} + \frac{2R_o(2+\nu)}{R_o+R_i})}$$

I don't know your properties of your rubber, but this would be the force required to close the rubber down to a 0 inside radius. As $R_o \to 2R_i$ (which is what the pictures look like), and for most rubbers, $\nu = 0.5$, so

$$ \text{Total Closing Force} = (\text{Volume of Rubber Ring}) . \frac{18E}{23 R_i}$$

As you can see, if the rubber has a somewhat normal modulus (Engineering Toolbox cites values on the order of 10 - 100MPa, I'll use 100 MPa below) - the closing force gets crazy high.

Fortunately, the action of the wedge reduces this force. Most of this force is taken by the cylindrical wall due to the angle. So, the pressurizing force would be $\cot(Big.Angle)$ times this force, for whatever that angle is. If we run with 60 degrees, then

$$\text{Total Pressurizing Force} = 40.52\ \text{MPa}\ (\frac{\text{Volume}}{R_i})$$