How to calculate the bending resistance of a square metal bar?

Question

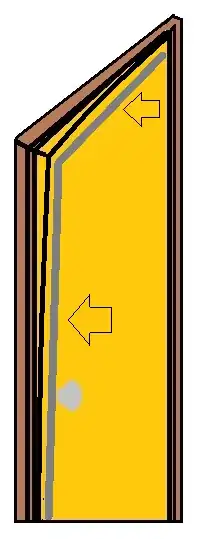
I have an old bend/twisted wooden door. It has some character to it so I want to keep it and add square metal bars to straighten it. I have provided a sample drawing of the door and where it is twisted. I have drilled a hole in the upper most open part and if I pull with a scale I am able to straighten it with about 20kg (I haven't used a scale yet, but I will)

I intend to put square metal bars on the bent sides (maybe even inside and out) and straighten the wood.

My question is what is the formula that I can use to calculate the size of the metal bar? For example I see there is a square profile bar 40x40x3mm that I will be able to buy and attach. So, is this going to be enough for the long side 2m and for the short side 1m? I can also order this square profile bar to be slightly bent and attach it so the two bends - the one of the wood and the one of the metal counter each other. But I am not really willing to go that way. I think its way too complicated.

Thank you in advance.

Edit:

1. I think a visible rectangle bar on one or both faces will be stronger and more simple to attach, so I will go with that.
2. No bend is acceptable - I want it straight.
3. So the next question following the comment is how much of a bend do I need for what type of bar for each of the sides - short(1m) and long (2m)?

Answer 1

If you estimate force needed to straighten the door applied at the corner is 20kg, it would be equivalent to the reaction of a uniformly loaded beam (your square bar) at one end.

So lets design the bar and for simplicity only the top bar, we can do the side later if we need to.

Lets say the door stays out of door jamb 2cm at the corner. So now we have all the data to design a bar or strap that has a deflection, built in bend, of 1/2 times 2cm =1cm and the 2 end reactions of 20kg, which for a 1m long strap mean omega is 40kg/m.

Deflection in a simply supported strap:

$$\delta = \frac {5 }{384 } \frac {\omega L^3}{EI} $$ This means $$0.01 = 5/384 \times40\times 1^3/(200GPa\times I)$$ $$ 2GPa\times I = 5/384\times 40 $$

This Gives the second moment, "I" of your strap and from there you can select the section of the bar that gives you optimal looks and required strength. Again this bar need to have a camber of 1cm built into it, so that after you attach it the door will be pressed into straight line.