I have a structure like such:
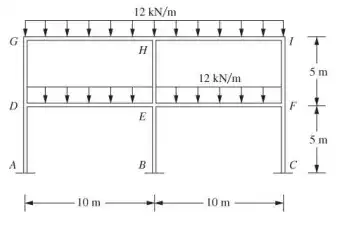
Due to my lack of knowledge of ANSYS, I have made the singular distributed loading (GI) represented as two distributed loadings (GH and HI).
Would this be an accurate model?
I feel like there should be some bending in the middle (HE to EB).
When I model it is a singular 240kN force on the center points I get:
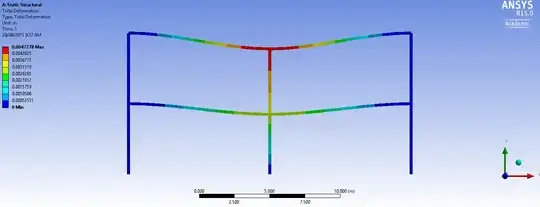
Which of these would be more accurate?
Splitting a uniform load into separate pieces that are still continuous will have no effect. This is frequently done.
As far as your question about bending in HE and EB, there shouldn't be any bending because all of the forces are balanced. A sum of the moments at H or E will show that the moments from the beams on either side are opposite and equal. That means that the resulting moment at the joint is zero.
To answer your added question, a single point load is not a replacement for the distributed load. The distributed load causes bending in the horizontal members. The distributed load also distributes load to the vertical members on each side. The single concentrated load focuses all of the force in the central column.
I would expect the modeling as a single load to be accurate. Force per linear area is the same expressed either way. You could look at a linear load on a single beam and just add more points of integration analytically and try it in ANSYS to see it.
The HE and BE segments will undergo buckling as its deformation mechanism after modest compression. The single load would logically be larger in aggregate since it is also applied to the small area supported directly by HE, but an eyeball examination says that this will be negligible and not affect the prediction that buckling is what you watch for in HE and BE. Are G, I, D, and F constrained in the model or free to move? Could affect buckling strength.
Adding just a slight notion:
Your experience would always expect the beam HE to buckle, because it is a Eulerian buckling beam (don't know if it's also called like this in English). The numeric only sees an evenly distributed load, so there will be no buckling... Try to alter your forces to the left and right of H a bit and you will get a moment which will cause HE to bend (If its support is rigid).
