In the general theory of 3D elasticity, there is no need for rotation variables.
However many engineering structures such as shells and beams have one or two dimensions that are small compared with the others. Representing the behaviour through the "thin" dimension as the difference between the translational displacements at the "top" and "bottom" surfaces is very badly conditioned numerically. To overcome that problem, the behaviour can represented approximately as the translation of the mid-plane (or more generally, the "neutral axis" of the object), and the slope (or rotation) of the cross section.
A simple example of this type of approximation is Euler-Bernouilli beam theory.
The formulation for shells and plates are similar in principle, but more complicated because the shell itself may be curved in one or both directions (e.g. part of a cylinder or a sphere).
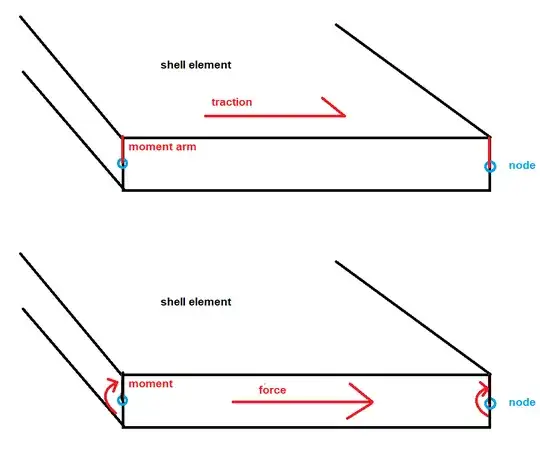
The reaction "force" corresponding to a constrained rotation variable is a moment - i.e. the finite value of the product $Fd$ when two equal and opposite forces $F$ are separated by a distance $d$, in the limit as $F$ increases to infinity and $d$ decreases to zero.
These approximations are useful in most engineering situations because of St. Venant's principle, which says that the overall response of a structure does not depend on the exact details of how the loads are applied, so long as the different applied loads are statically equivalent.