4

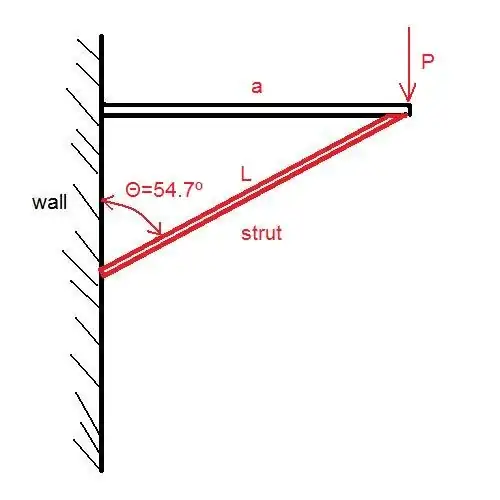
I want to affix a cantilever to wall. I will support the other end of the cantilever with a strut made of wood, that attaches to some point on the wall below the cantilever, as shown in this sketch (click for full resolution):

At what angle will the strut provide the greatest vertical strength/support for the free end of the cantilever?

Kreeverp
  • 143
  • 1
  • 1
  • 5

2 Answers2

8

Assumptions

  • The angle between the wall and the strut is $\theta$
  • $a$ is the depth of the table top
  • $P$ is the weight on the table top, applied at the edge furthest from the wall
  • The strut will fail when it buckles, which implies $F_{\text{max}}=\frac{\pi^2EI}{L^2}$ where $L$, $E$ and $I$ are the length, the elastic modulus, and the moment of area, respectively, of the strut

Analysis

The axial force on the strut will be $F=\frac{P}{\cos\theta}$. The length of the strut will be $L=\frac{a}{\sin\theta}$. Combining both equations with the equation for buckling we have: $(EI)_{\text{required}}=\frac{Pa^2}{\pi^2\sin^2\theta \cos\theta}$.

$EI$ is the stiffness of the strut. The most efficient strut will be one for which $(EI)_{\text{required}}$ is minimized. The lowest $(EI)_{\text{required}}$ occurs when $\sin^2\theta \cos\theta$ is maximized and that is when $\theta=\sin^{-1}\sqrt{\frac{2}{3}}$ so the most efficient angle is $\theta\approx54.7^{\circ}$ strut

wythagoras
  • 109
  • 6
Mandrill
  • 356
  • 1
  • 4
0

I had a school assessment and decided to look into this. I believe you have calculated the angle that results in the least stiff strut - not the strongest. I would like to think that a higher moment of inertia (I) is better as it reduces the effect that force has on the rotation of the strut - this contradicts your answer. Yet you are correct in saying that a reduction in E the modulus of elasticity is better for the structures strength. I believe that this demonstrates the fact that this problem requires a better solution somewhere between 54.7 and 0 degrees because we do not just want to minimise EI but find a balance. Here is my reasoning/approach to the problem: the theoretical most optimal angle is 0, as theta approaches 0 and the side lengths extend to infinity and simulate a bridge or 2 fixed points (most optimal). this does not take into account the material weight and hence is unreasonable. for anyone looking into this as-well I would think angles of 45 or less to be optimal. Please (logically) correct me if I am wrong.

Plants Are us
  • 1