Equations of Motion
From what I understand from the question and your comments, you can write the equations of motion of the 3-dof oscillator in the form:
$$M \frac{d^{2}x}{dt^{2}} + C \frac{dx}{dt} + K x = f$$
where the vector $x$ represents the displacements, $M$, $C$ and $K$ are the mass, damping and stiffness matrix respectively, and $f$ is some forcing vector (e.g. impact, step function, etc.). Therefore, this type of equation may be classified as a Linear Time-Invariant (LTI) system.
Damping models
There are several ways to solve this type of LTI systems, for instance numerical time integration, and as mentioned in the response by @am304, different models to represent the damping matrix $C$.
Rayleigh damping is indeed one form:
$$C = aM + bK$$
where parameters $a$ and $b$ are chosen arbitrarily. You could also use modal damping, which is similar and may be written in the form:
$$V' C V= 2 x_iW$$
where $W$ is a diagonal matrix containing the linear eigenvalues of your system, $V$ the associated eigenvectors and $x_i$ is the damping coefficient (which may vary from mode to mode but can be considered as a single constant as a first approximation). The main advantage of this method is that the damping carries with it the inherent dynamics of your linear system and is diagonal in the modal domain.
Performance
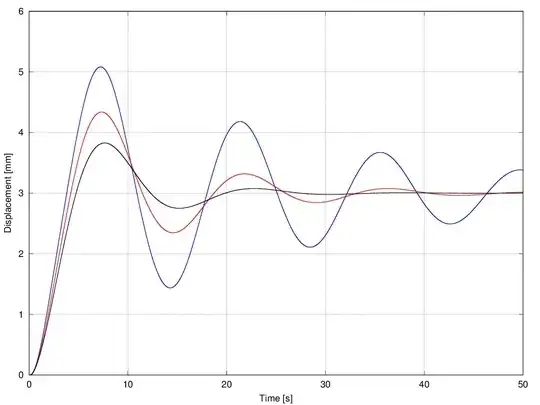
In terms of performance, with respect to the overshoot and the settling time, they will be both dependent on the damping term as well as the stiffness, since the two quantities are related in the two modeling strategies here proposed. However, for a given stiffness matrix, the solution will reach a steady-state with a specific amplitude, and the overshoot and settling time will solely depend on $x_i$ as shown in the picture below (Last mass displacements for: $x_i=0.2$ (blue), $x_i=0.5$ (red) and $x_i=0.8$ (black)).