3

I am in the process of completing a design project for my fluids course in which Buckingham-Pi /Dimensional Analysis is needed to find the optimal parameters needed to achieve a rotational rate of 120 rpm.

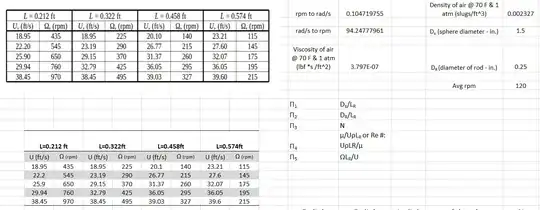
So the question at hand is that the rotational rate of an anemometer is a function of density, viscosity, wind speed, rod length, sphere diameter, rod diameter, and number of spheres.

[Omega = f(rho,mu,Ds,Dr,Lr,N,U)] and from that we need to non-dimensionalize the parameters and get Pi groups in which we analyze and determine the optimal dimensions required to achieve a rotational rate of 120 rpm.*

enter image description here

I have met with the professor regarding the project and I was told that the dependent variable (group with the omega) is to be plotted on the y axis against all other groups (independent Pi groups on the x axis). He also mentioned that rho, and mu are parameters because the same results should occur regardless of the fluid used in testing.

**I have worked out the problem and have achieved the Pi Groups and even plotted them; but I do not know how to account for the the non-dimensional value N( # of spheres); or what needs to be done next. **

All work for Pi-Groups

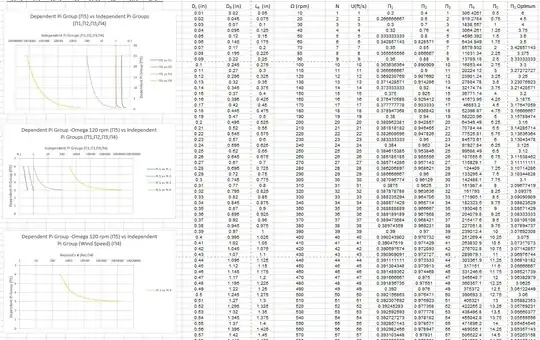
enter image description here enter image description here

Graphs/Excel Stuff

I chose random ranges that fit within the spec so is that even correct to get some data points to graph so can you do that?

(All pi groups which use rho and mu, are plugged in as the values at the top since I'm not sure what range to use for them since it can be any fluid, so not sure if my approach is even remotely correct?).

NOTE : Pi (4) when plotted was taken to be the Reynolds's # which is the inverse of the computed Pi group (I mention this on excel spreadsheet).

*First graph is dependent pi group (5) against all other pi groups.

*Second is with the avg rotational rate of 120 rpm as the parameter for the dependent pi group (5).

*Third is just wind speed Pi group (4) against omega dependent pi group (5).

enter image description here enter image description here

Have a look and let me know if I'm doing something wrong/right.

Any and all help is appreciated :)

John Giannopoulos
  • 31
  • 1
  • @JeffreyJWeimer not sure what you mean? Yes that’s true; there needs to be some gradient or some reason for a fluid to move but in this specific case dimensionality and similitude between parameters and the model which was experimentally tested needs to be used in order to find the optimal parameters to achieve an rpm of 120; right? – John Giannopoulos May 13 '19 at 21:18
  • Isn’t the flow of fluids developed from a force or an energy balance? Both are related to pressure. Would that not suggest to you that force per area will drive the system somehow? Yet all of your dimensional terms are essentially one dimensional. Nothing accounts for area. Your cups could just as well be toothpicks. – Jeffrey J Weimer May 13 '19 at 21:19
  • I have added to the third pi group where N (Number of Spheres) is related to a torque where the force is P*A where P is 1 atm or 14.7 psi and A is pi/4 ds^2. It’s moment arm is (rod length/2) x PA (F) and the angular velocity (omega) multiplies by the torque to give a Power. Their needs to be some external relationship tied to in order to use similitude or so I’ve heard from my professor; is that true- or is a dimensionless parameter dealt with some other way? – John Giannopoulos May 13 '19 at 21:26
  • I know for sure that the parameters are correct since there are supposed to be 4 and one non dimensional parameter (N) pi groups. So 5 total pi groups and the parameters all make sense for the most part; and the angular velocity (omega) all depend on the parameters so isn’t my function of omega correct? – John Giannopoulos May 13 '19 at 21:36
  • I suggest only that you consider the fundamental insights using your chosen parameters that completely ignore the area of the cops and prefer instead to use their length. To cast this a different way, even though we can derive an equation that is fully correct for the stated assumptions, we will still fail to solve the problem when the assumptions themselves are entirely wrong. In this regard, I suspect that your efforts may be heading down the wrong road right from the outset. – Jeffrey J Weimer May 13 '19 at 23:06
  • How would I go about the question correctly? I know that for sure the parameters are correct and Pi groups are required so what exactly am I doing wrong. I’m very confused and want some type of guiding light to answer the questions presented which are: how do you take care of a dimensionless parameter in a pi group and how do you plot them correctly and thus get some insight to solve the prototype dimensions for an omega of 120 rpm. – John Giannopoulos May 13 '19 at 23:35
  • Bluntly put, what does the analysis give when you use the areas of the cups (and perhaps also the rods) rather than their lengths as fundamental parameters? – Jeffrey J Weimer May 14 '19 at 00:55
  • Did you solve this problem? – Armadillo Jan 05 '23 at 15:51

1 Answers1

1

Let's assume that you will work out the right combinations of dimensionless terms on your own. Let's consider only the question of what to plot once you have those terms. By example, in heat transfer, the Nusselt number $Nu$ is for forced convection is a function of the Reynolds number $Re$ and the Prandtl number $Pr$. In this case we can make one of two general plots.

  • Plot $Nu$ versus $Re$ for fixed values of $Pr$. This is equivalent to tracking the effects of fluid velocity for a fixed type of fluid.
  • Plot $Nu$ versus $Pr$ for fixed values of $Re$. This is equivalent to tracking he effects of different types of fluids at the same flow velocity.

Suppose later that, using further analogies in laminar flow, we predict that $Nu = C Pr^{1/3}Re^{1/2}$. We can revise our plots to be "linearized".

  • Plot $Nu$ versus $Re^{1/2}$ for fixed values of $Pr$. This is equivalent to tracking the effects of fluid velocity for a fixed type of fluid.
  • Plot $Nu$ versus $Pr^{1/3}$ for fixed values of $Re$. This is equivalent to tracking he effects of different types of fluids at the same flow velocity.

Finally, with the assumption that only two parameters influence this system, we can write

$$ d Nu = \left(\frac{\partial Nu}{\partial Re}\right)_{Pr} d Re + \left(\frac{\partial Nu}{\partial Pr}\right)_{Re} d Pr$$

The partial derivatives are the slopes of the curves on the respective plots. Absent a theoretical equation, we can use the above equation and the graphs to predict which term has the greater influence on $Nu$. By example, when we ant to increase $Nu$ for the case when

$$ \left(\frac{\partial Nu}{\partial Re}\right)_{Pr} > \left(\frac{\partial Nu}{\partial Pr}\right)_{Re}$$

we predict that we will do better to increase $Re$ (e.g. increase the flow velocity for the given fluid) than to increase $Pr$ (e.g. change the fluid at the same flow).

Jeffrey J Weimer
  • 3,021
  • 8
  • 16