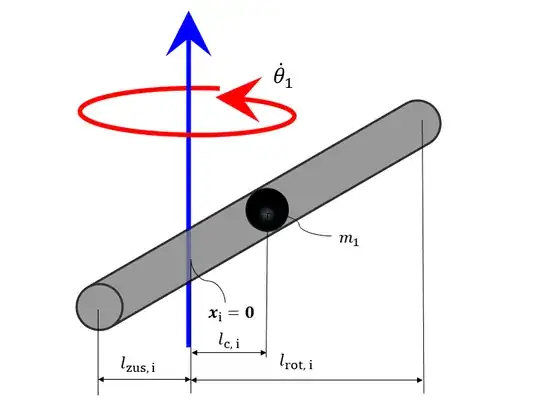
I want to express the inertia tensor of a rotating rod (total length $L_1$) to use it in Lagrange mechanics for expressing the kinetic energy associated to the rotation with angular velocity $\dot{\theta}_1$. I know the moment of inertia regarding the center of mass $m_1$ as $1/12\cdot m_1 L_1^2$ and with the central axes theorem I obtain $$ J_{1yy} = J_{1zz} = 1/12\cdot m_1 L_1^2 + m_1 l_{c,1}^2 $$ So I can express the the kinetic energy as $$ 1/2 \cdot \dot{\theta}_1^2 (1/12\cdot m_1 L_1^2 + m_1 l_{c,1}^2) $$ Is that right?
The rotation is constrained to the horizontal plane around the origin ($\vec{x}_i = \vec{0}$)