How do I calculate the density of seawater at different temperatures?

Question

I need to know the difference in seawater density at 28 and 98 degrees Fahrenheit for control system synthesis. How can I calculate the density for a given temperature?

Answer 1

The density depends not only on temperature, but also on salinity, see the wikipedia page on seawater, which has this neat diagram:

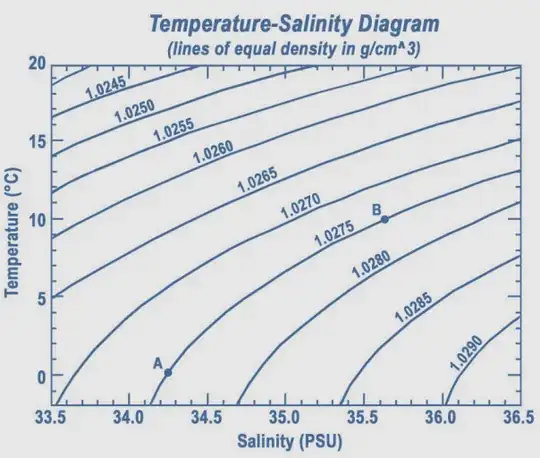
Assuming you have seawater of constant salinity, you can use the above graph to get your answer by drawing a vertical line at the corresponding salinity value. The intersections of that line with the lines of equal density will give you your data points of density vs. temperature. Read the value of the density from the line you are intersecting and find the corresponding y-value to get the temperature.

Once you have your data points of density vs. temperature, you can then graph it and interpolate it for the desired temperature.

As an example, assuming a constant salinity of 35 PSU, I get the following data points:

density_35psu = [1.028 1.0275 1.027 1.0265 1.026 1.0255 1.025];
temp_35psu = [2 6.5 9.5 12.4 15.4 17.3 19.55];

which gives the following graph (I have fitted a second-order polynomial and extrapolated to the temperatures of interest):

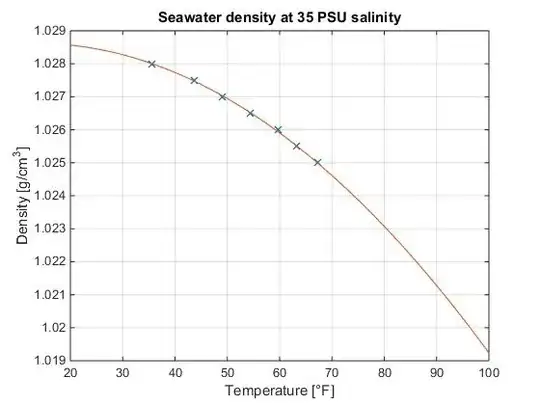
It gives me a seawater density of 1.0284 g/cm^3 at 28°F and 1.0197 g/cm^3 at 98°F.

Answer 2

You could use the Equation of State for seawater. Sources and detailed information on this topic are to be found here, here and here.

Please note that the equation apparently does not cover temperatures below freezing point.

Equation of State for Seawater

$(\rho - \rho^0) = AS_A + BS^{1.5}_A + CS^2_A$

$\rho^0$ is the densitiy of pure water.

With

$A = a_0 + a_1T + a_2T^2 + a_3T^3 + a_4T^4 + a_5T^5$

$B = b_0 + b_1T+ b_2T^2$

$C=c_0$

Units

$[ \rho ] = \frac{kg}{m^3}$

$[ T ] = °C$

Experimentally-determined parameters for calculating $A$ and $B$ can be taken from Table 2 in the Ocean Science paper (F. J. Millero and F. Huang , 2009):

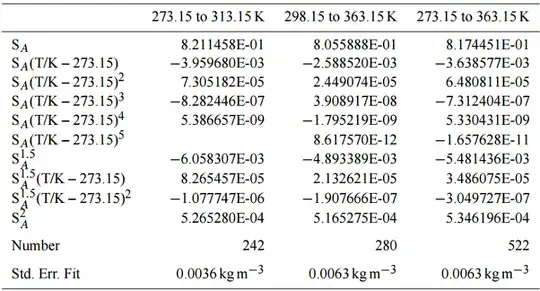
The table shown here is found in the corrigendum to the linked paper, not the paper itself.