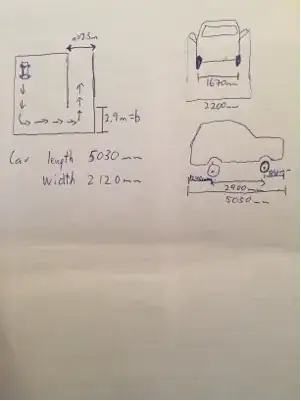
To slightly generalize I'll reform the question slightly.
A ridged 2-D body (car) has a line $l$ that moves with it.
The car can be linearly transformed as long as the instantaneous center of rotation lies along $l$ at least distance $R$ away from a point $c$ that also moves with the car.
In this case point $c$ lies in the center of the rear axle and $l$ lies on the rear axle.
Now imagine the car's domain is limited to a quarter plane with edges $A$ and $B$. It initially is placed against $A$, far from $B$ with $l$ perpendicular to $A$, and the goal is to translate the car so that it is against $B$ far from $A$ while minimizing the maximum distance from the closest edge.
($A$ and $B$ can be placed a inch away from the actual walls to prevent scratches and allow for non-idealized vehicle movement.)
Reversals allowed
The solution is to advance the car along $A$ until it is an infinitesimal distance from $B$ (using an infinite turning radius to travel in a straight line) Then rotate about the tightest turning radius until in contact with $B$ Then rotate about the tightest turning radius on the opposite side until back in contact with $A$. This results in linear movement in the opposite direction but rotation in the same direction. These two steps can be repeated (infinitely) until $l$ is perpendicular to $B$ at which point it can advance away from $A$ in a straight line. From a macro perspective this looks like the car sliding along $A$ until it reaches $B$, then rotating while maintaining contact with both walls and finally advancing along $B$. This solution is independent of turning radius but involved infinite reversals.
No reversals
Now lets further constrain our translations so that center of rotation must be further from $A$ and $B$ than $c$. (This removes the usefulness of backing up)
Now the middle of the optimum strategy is obvious: turn at the maximum turning radius, but how do you minimize the distance to the wall approaching and exiting this strategy?
You remain in contact with the wall.
As you approach the wall and see you're just about to clear it, rather than continuing to turn you can gradually increase the turning radius to remain in contact with the wall. To remain in contact with the wall means the line between the contact point and the center of rotation is perpendicular to the wall.
From this we can get the position of the center of rotation while in the minimum turning radius portion of the turn.
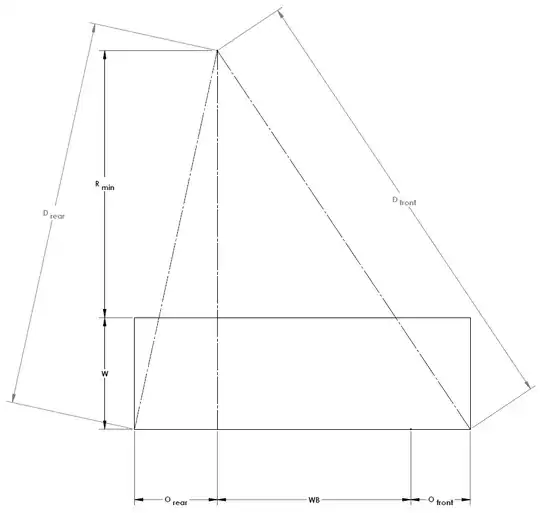
$$D_{rear}=\sqrt{{O_{rear}}^2+(R_{min}+W)^2}$$
$$D_{front}=\sqrt{(O_{front}+WB)^2+(R_{min}+W)^2}$$
This point fully defines the most interesting portion of the turn allowing one to see if any obstacle on the other side would be struck. To clear:
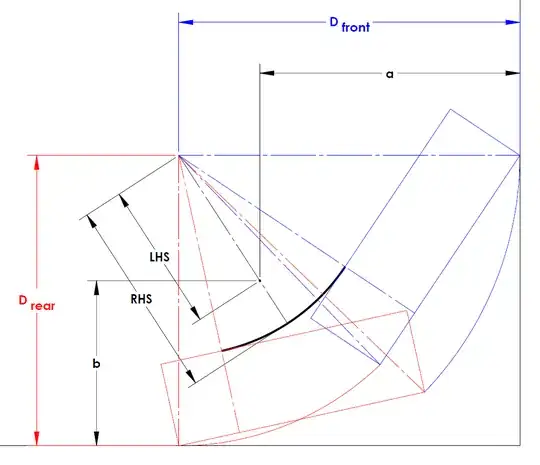
$$\sqrt{(D_{rear}-b)^2+(D_{front}-a)^2} \leq R_{min}$$
Note that it makes a difference if you're going forward or backward. To see if you'd clear both directions you'd have to test with a and b reversed.
Indeed in the diagram above I've set $a=5.9m$ and $b=3.3m$. In this case it was because while the thick arc defined by drawing and equations above might be the most interesting portion of the curve, it is not going to be the limiting factor when $a$ and $b$ are not flipped. So we need to extend that curve.
The end points can be found using similar triangles, from there, the curve will just be an tangent exponential decay to a distance $W$ from the wall.
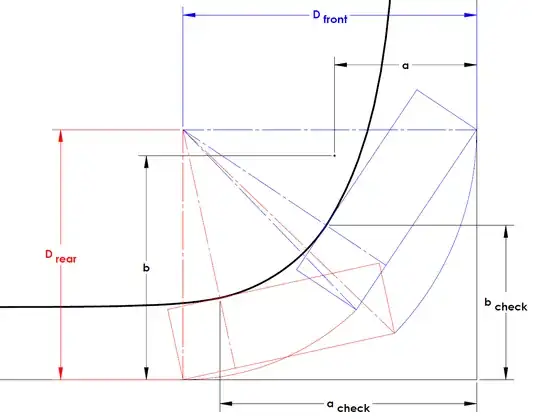
With these curves we can define a function $C$ to tell us whether the vehicle would clear an object placed at $(a,b)$:
$$
C(a,b) =
\begin{cases}
\hfill \sqrt{(D_{rear}-b)^2+(D_{front}-a)^2} \leq R_{min} \hfill & \text{ if } a \leq a_{check} \text{ and } b \leq b_{check} \\
\hfill W+W_{rear}e^{\frac{(a_{check}-a)O_{rear}}{(R_{min}+W)W_{rear}}} \leq b \hfill & \text{ if } a > a_{check} \text{ and } b \leq b_{check} \\
\hfill W+W_{front}e^{\frac{(b_{check}-b)(O_{front}+WB)}{(R_{min}+W)W_{front}}} \leq a \hfill & \text{ if } a \leq a_{check} \text{ and } b > b_{check} \\
\hfill true \hfill & \text{ if } a > a_{check} \text{ and } b > b_{check} \\
\end{cases}
$$
Where:
$$a_{check}=D_{front}-O_{rear}\frac{R_{min}}{D_{rear}}$$
$$b_{check}=D_{rear}-(O_{front}+WB)\frac{R_{min}}{D_{front}}$$
$$W_{front}=D_{front}-(R_{min}+W)\frac{R_{min}}{D_{rear}}-W$$
$$W_{rear}=D_{rear}-(R_{min}+W)\frac{R_{min}}{D_{front}}-W$$
Now to solve this system backwards to get the maximum $R_{min}$ that would allow passage requires making a few observations and assumptions. First we'll assume that you want to be able to drive around the corner in ether direction that means we'll swap $a$ and $b$ for whichever scenario is worse. If The front corner is further from the fixed axle than the rear corner (as is the case for all front steering vehicles I know of) then a < b is the tighter scenario.
Then one could use a numerical method to find the $R_{min}$ that gave equality for the second inequality. If $a\geq a_{check}$ then you're done. If not, then find the $R_{min}$ that gives equality for the first inequality.
Glossary
- $W$ - Width of car
- $WB$ - Wheel Base
- $O_{front/rear}$ - Overhang of the front/rear
- $R_{min}$ - minimum distance between the center of rotation and the car
- $a$ - distance from outside wall to inside corner
- $b$ - distance from outside wall to inside corner
Plugging in
With the numbers given It turns out that the maximum $R_{min}$ is slightly under $6.6m$
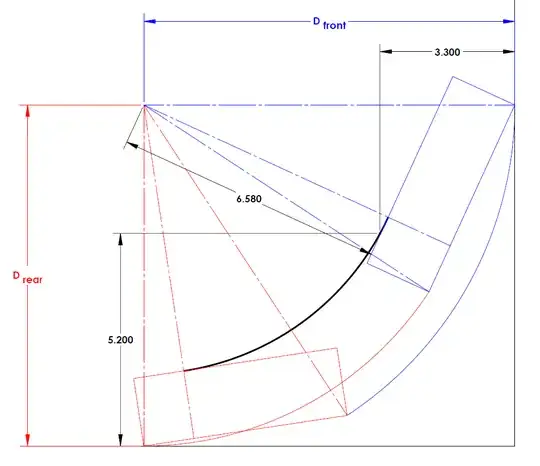
But you might have to fold the right mirror in.